Statistical mechanics of fluids

General exprssion of probability distribution of fluids in phase space¶

The probability of a state in a classical fluid system is $f(x^N, p^N)$

{f(x^N, p^N) = \frac{e^{-\beta H(x^N p^N)}}{Z}}

(1)

Momentum and position coordinates are separated thanks to the form of kinetic and potential energy terms

H(x^N, p^N) = K(p^N) + U(x^N)

(2)

f(x^N, p^N) = \Phi(p^N) P(r^N)

(3)

Kinetic energy part giveus us Maxwell-Botlzman distribution or the ideal gas part of the partition function $Z_p$
Potential energy part gives us configruational parition function $Z_x$ evaluation of which is non-trivial and mostly can be done via simulaions:

Z(\beta, V, N) = Z_{p} \cdot Z_x = \frac{1}{\lambda^3 N!} Q(\beta, V, N)

(4)

Q = \int dx^N e^{-\beta U(x^N)}

(5)

Pressure is related to Free energy as

p= - \frac{\partial F}{\partial V} = \frac{\partial }{\partial V} log \int dx^N e^{-\beta U(x^N)}

(6)

Volume dependence of partition function is in the integration limits! As volume grows, so does partition function. Therefore p is always positive. We can thus conclude that in equilibrium pressure is always a positive quantity

Reduced configruational distribution functions¶

Key fact: The full configurational probability $P(r^N)$ and the partition function $Q$ do not factorize due to interparticle interactions. Stronger interactions lead to stronger positional correlations.
Joint probability of particle positions:
To describe the probability of finding particles at positions $r_1, r_2, \dots, r_N$ :

{P(r^N) = P(r_1, r_2, \dots, r_N)}

(7)

Marginal (reduced) probability density:
Probability of finding particles 1 and 2 at positions $r_1$ and $r_2$ , regardless of others:

{\rho^{(2)}(r_1, r_2) = \int dr_3 \dots dr_N \, P(r^N)}

(8)

Symmetrized reduced pair distribution:
When particles are indistinguishable, the reduced two-particle distribution becomes:

{\rho^{(2)}(r_1, r_2) = N(N-1) \int dr_3 \dots dr_N \, P(r^N)}

(9)

Radial Distribution Function (RDF)¶

For an isotropic fluid, the one-particle probability density is uniform:

\rho^{(1)} = N \frac{\int dr_2 \dots dr_N}{\int dr_1 \dots dr_N} = N \frac{V^{N-1}}{V^N} = \frac{N}{V} = \rho

(10)

For an ideal gas, the two-particle (joint) probability density simplifies as:

\rho^{(2)} = N(N-1) \frac{\int dr_3 \dots dr_N}{\int dr_1 \dots dr_N} = N(N-1) \frac{V^{N-2}}{V^N} \approx \rho^2

(11)

To quantify spatial correlations between particles, we define the Radial Distribution Function (RDF) as:

{g(r_1, r_2) = \frac{\rho^{(2)}(r_1, r_2)}{\rho^2}}

(12)

For an isotropic and homogeneous fluid, RDF depends only on the distance between particles:

{g(r) = g(|r_2 - r_1|)}

(13)

Physical meaning of RDF¶

Since $\rho = \rho^{(1)}$ , the conditional probability density of finding a particle at distance $r$ from a tagged particle at the origin is:

\frac{\rho^{(2)}(0, r)}{\rho} = \rho g(r)

(14)

Thus, $\rho g(r)$ represents the average local density at distance $r$ , given a particle is fixed at the origin.

import numpy as np
import matplotlib.pyplot as plt

# === System parameters ===
N_side = 20                # particles per side for lattice
N = N_side**2              # total particles
L = 10.0                   # box length (L x L)
r_max = L / 2              # max distance for RDF
nbins = 100

# === Make ideal gas configuration ===
positions_ideal = np.random.uniform(0, L, size=(N, 2))

# === Make square lattice configuration ===
spacing = L / N_side
x, y = np.meshgrid(np.linspace(0, L - spacing, N_side),
                   np.linspace(0, L - spacing, N_side))
positions_lattice = np.vstack([x.ravel(), y.ravel()]).T

def compute_rdf(positions, L, r_max, nbins):
    N = len(positions)
    dists = []
    for i in range(N):
        for j in range(i + 1, N):
            dx = positions[i, 0] - positions[j, 0]
            dy = positions[i, 1] - positions[j, 1]
            
            # Periodic boundary conditions
            dx -= L * np.round(dx / L)
            dy -= L * np.round(dy / L)
            r = np.sqrt(dx**2 + dy**2)
            if r < r_max:
                dists.append(r)
    
    dists = np.array(dists)
    r_bins = np.linspace(0.0, r_max, nbins + 1)
    r_centers = 0.5 * (r_bins[:-1] + r_bins[1:])
    hist, _ = np.histogram(dists, bins=r_bins)
    
    dr = r_bins[1] - r_bins[0]
    area = L**2
    rho = N / area
    shell_area = 2 * np.pi * r_centers * dr
    norm = rho * shell_area * (N - 1) / 2  # expected number in each shell
    g_r = hist / norm
    
    return r_centers, g_r

# === Compute RDFs ===
r_ideal, g_ideal = compute_rdf(positions_ideal, L, r_max, nbins)
r_lattice, g_lattice = compute_rdf(positions_lattice, L, r_max, nbins)

# === Plot ===
plt.figure(figsize=(8, 4))
plt.plot(r_ideal, g_ideal, label='Ideal Gas', lw=2)
plt.plot(r_lattice, g_lattice, label='Square Lattice', lw=2)
plt.axhline(1.0, color='gray', linestyle='--')
plt.xlabel('Distance $r$')
plt.ylabel('$g(r)$')
plt.title('Radial Distribution Function Comparison')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

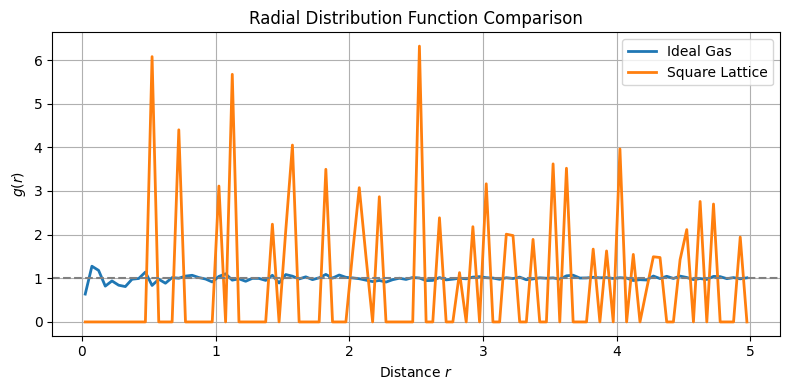
Coordination shells and structure in fluids¶

Reversible work theorem and potential of mean force¶

\Big \langle -\frac{d U(r^N)}{dr_1} \Big \rangle_{r_1, r_2} = -\frac{\int dr_3...dr_N \frac{dU(r^N)}{dr_1} e^{-\beta U}}{\int dr_3...r_N e^{-\beta U}} = \frac{\beta^{-1} \frac{d}{d r_1} \int dr_3...dr_N e^{-\beta U}}{\int dr_3...dr_N e^{-\beta U}} = \beta^{-1} \frac{d}{d r_1} log \int dr_3...dr_N e^{-\beta U}

(17)

\Big \langle -\frac{d U(r^N)}{dr_1} \Big \rangle_{r_1, r_2} = \beta^{-1} \frac{d}{d r_1} log N (N-1)\int dr_3...dr_N e^{-\beta U} = \beta^{-1} g(r_1, r_2)

(18)

Thermodynamic properites of $g(r)$ ¶

\langle E \rangle = N \Big\langle \frac{p^2}{2m} \Big\rangle + \Big\langle \sum_{j>i} u(|r_i - r_j|)\Big \rangle

(19)

{E/N = \frac{3}{2}k_B T +\frac{1}{2}\rho \int dr g(r) u(r) }

(20)

Low density approximation for $g(r)$ ¶

w(r) =u(r) +\Delta w(r)

(21)

g(r) = e^{-\beta u(r)} \Big (1 +O(\rho) \Big)

(22)

Density expanesion and virial coefficients¶

\beta p = \rho + B_2(T) \rho^2+ O(\rho^3)

(23)

B_2(T) = -\frac{1}{2} \int dr (e^{-\beta u(r)}-1)

(24)

Statistical mechanics of fluids

General exprssion of probability distribution of fluids in phase space¶

Reduced configruational distribution functions¶

Radial Distribution Function (RDF)¶

Physical meaning of RDF¶

Coordination shells and structure in fluids¶

Reversible work theorem and potential of mean force¶

Thermodynamic properites of g(r)g(r)g(r)¶

Low density approximation for g(r)g(r)g(r)¶

Density expanesion and virial coefficients¶

Thermodynamic properites of $g(r)$ ¶

Low density approximation for $g(r)$ ¶