Review of thermodynamics principles

Extensive vs Intensive variables¶

• Extensive variables: Depdent on System size These are fundamental variables that uniquely define the equilibrium states. Examples are $V, N, E, S$.

• Intensive variables: Size Independent These are derived from the extensive ones and are considered as conjugate pairs. E.g $V-P$, $N-\mu$ and $S-T$, are conjugate pairs.

• Intensive variables do not have the same fundamental status as extensive variables

  • Because they do not always uniquely describe the state of matter in equilibrium.

  • For example, a glass of water with and without an ice cube can be under 1 atm and 0 C, whereas energy and entropy volume values will differ.

Equilibrium and thermodynamic space¶

<img src="./figs/adiabat.png" class="bg-primary" width="300px">  

A and B are equilibrium states. A quasistatic process connecting A and B is in the thermodynamic space (however, see the warning in the text). From A to B a process need not be quasistatic. Then, most such processes are outside the thermodynamic space (broken curve).

• Equilibrium refers to a state of matter which is unchanging. There are no macroscopic fluxes or flows of energy or matter.

• The state of Equilibrium is defined relative to observation time! A glass of water on the table is in a state of equilibrium on the time scale of minutes but in a state of non-equilibrium over the scale of days because water evaporates, changing the thermodynamic state of the glass.

• Euilibrium is represented as a point in the Thermodynamic space $E(X_1, X_2, ...)$ where $X_i$ are extensive variables.

  • These coordinates have unique and well-defined values for each equilibrium state irrespective to how such state was created.

  • Intensive variables become ill-defined if the system is not in equilibrium (temperature, pressure, etc).

  • Functions like energy $E$ are called state functions, and their changes are given by differences between initial or final state only $\Delta E =E_f -E_i$.

  • On the other hand one can have quantities such as work $W$ or heat $Q$. These are path dependent characterizing the way energy is transferred to the system and not characterizing equilibrium states!

Fundamental equation of thermodynamics¶

• Transformations between equilibrium states is the central task of thermodynamics. Knowing the fundamental equation, one can predict the equilibrium state B, which results from equilibrium state A through spontaneous transformation upon removal of a constraint. E.g computing $\Delta E = E_B - E_A$ given expansion of a box.

• Quasi-static path: a dense succession of equilibrium states that connects A with B in extensive variables is constructed to compute changes in thermodynamic variables between states A and B. The quasistatic process ensures the system does not deviate from the equilibrium state during transformation.

• Reversible transformations can go forward or backward without any change in the environment. This necessitates the introduction of Entropy, which differentiates reversible from non-reversible changes.

• The quasistatic path may or may not be reversible Just because the process is infinitely slow and locally in equilibrium does not make it reversible along the path of transofrmation. For instance, poking a small hole in a container and letting one molecule out very slowly does not make the process reversible.

First Law¶

Note on signs

• By convention sign of work or heat is positive if energy is transfered to the system. Negative if it system loses energy. Hence think about signs from the perspective ofa system under study.

• If engine does work against external pressure $p$ then $dW= -pdV$. You can see work is going to be negative for expanding volume $dV>0$ and positive for contracting $dV<0$

• If system is absorbing heat from environment (heating up) $\delta Q>0$. If the system is refridgerating then $\delta Q<0$

Adiabatic Change $dQ=0$

No work

Adiabatic Processes¶

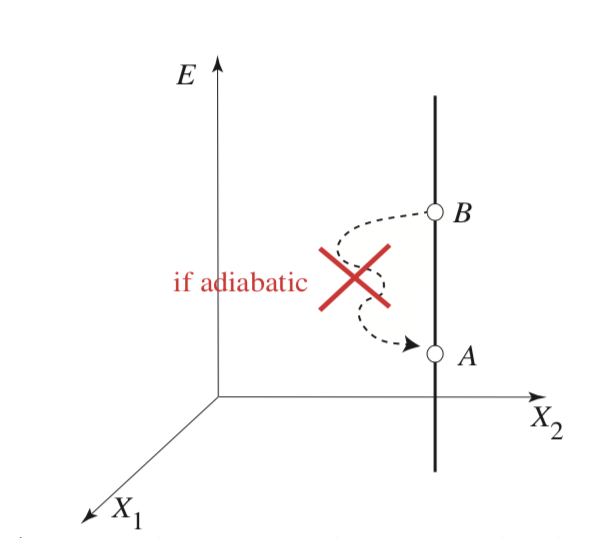
• Intuitively, this means that when performing pure mechanical work on a system, we can only impart energy to it due to friction or dissipation. Conversely, it is impossible to “steal” energy from a closed system purely through mechanical work without any accompanying environmental change.

• Consequently, not all paths in thermodynamic space are accessible; one cannot always transition freely from state A to state B. This suggests the existence of a fundamental constraint—possibly a new variable—that dictates when transitions are allowed and when they are not.

<img src="./figs/Adiabats.png" class="bg-primary" width="300px">  

Let Q be a state on a vertical line L (along which we can move with heat exchange alone) that can be reached from state P adiabatically and quasistatically. If state A can be reached by an adiabatic process from P, then adiabatically we can go from Q to A via P, violating Planck’s principle. Thus, the shaded portion is inaccessible from P adiabatically.
If state B can be reached by an adiabatic and quasistatic process from P, then adiabatically we can go from B to Q via P, violating Planck’s principle, again. Thus, Q is unique: there is only one point on L that can be reached from P adiabatically and quasistatically.

<img src="./figs/NO1.png"  class="bg-primary" width="200px"> 

If two adiabats cross or touch, then we can make a cycle that can be traced in any direction, because PQ and P’Q can be traced in either directions, so Planck’s principle is violated.

• This restriction implies that adiabatic surfaces (or lines) cannot intersect. If they did, one could design a cyclic mechanical process that decreases the system’s energy, violating the second law. Moreover, an intersection would imply that the same thermodynamic coordinates correspond to two different forces (energy derivatives), which is physically inconsistent.

  • Therefore, thermodynamic space is foliated by non-intersecting adiabats.

  • This structure naturally leads to the definition of an extensive variable, Entropy $S(E)$, which remains constant along each adiabatic surface and increases with energy across different adiabats.

  • Since entropy is a monotonic increasing function of energy $S(E)$, it follows that Planck’s formulation implies:

• However, as we shall see the entropy-based Second Law is more general, as it applies to both adiabatic and non-adiabatic transformations.

Reversible Heat Exchange¶

• Moving from one adiabat to another requires heat input or removal.

• This structure underlies entropy-based formulations of the Second Law, as entropy remains constant or increases in an adiabatic process.

• Here, we identify the prefactor as the temperature, which we will soon rediscover in statistical mechanics.

• Since mechanical manipulation alone does not move the system between adiabats, this implies that entropy can only be reduced by cooling ($dQ < 0$).

Second Law¶

• For general non-adiabatic case of system in contact with an infinitely large reservoir (heat bath) it is the entropy of the combined system+reservoir that must increase.

• The reservoir the entropy change is solely due to heat exchange $Q_r=-Q$

Understanding the Signs¶

• Irreversibility and Entropy Production

  • The inequality $dS > \frac{\delta Q}{T}$ captures entropy increase due to internal irreversibilities, such as:

  • Friction, viscosity, turbulence** in fluids. Non-equilibrium chemical reactions. Unrestrained (free) expansion

• Reversible Heat Transfer

  • The equality $dS = \frac{\delta Q}{T}$ holds when:

    • The system remains in thermal equilibrium with surroundings.

    • Heat exchange occurs infinitesimally slowly (e.g., between objects with an infinitesimal temperature difference).

• Equilibrium Condition:

  • Entropy is maximized $dS=0$ and no spontaneous changes occur:

Gibbs Relation¶

• The internal energy of a thermodynamic system can be expressed as a function of its extensive variables: entropy $S$, volume $V$, and number of particles $N$:

• Taking the total differential of $E$, we obtain:

• We identify the intensive variables conjugate to the extensive variables:

• Temperature $T$

  $$T = \left(\frac{\partial E}{\partial S} \right)_{V,N}$$

  (14)

• Pressure $P$

  $$P = -\left(\frac{\partial E}{\partial V} \right)_{S,N}$$

  (15)

• Chemical potential $\mu$

  $$\mu = \left(\frac{\partial E}{\partial N} \right)_{S,V}$$

  (16)

The first law of thermodynamics can then be written in its fundamental formm Texpressing how changes in entropy, volume, and particle number contribute to changes in energy.

Gibbs Duhem relation¶

• The extensivity property implies linear scaling with respect to extensive variables. In other words, extensive variables are additive quantities.

• Using chain rule we get a liner relationship between extensive variables not involving any differentials:

• When we take the derivative of E and compare with Gibbs relation we end up with equation where independent variables are now intensive ones

Entropy Maximization Principle¶

• When we release a constraint in an adiabatic system the extensive coordinates $X_i$ change. This spontaneous change must always lead to increase in entropy $\Delta S \geq 0$

• Entropy can increase until reaching its maximum possible value after which no further change is possible.

• A change in system entropy $\delta S$ due to any change or pertrubation is therefore telling us that

  • If $\delta S>0$ system spontaneously evolves

  • If $\delta S < 0$ system is thermodynamically stable (any change from maximum leads to decrease of entropy)

• Therefore the second law gives us a variational principle in terms of entropy to find stable equilibrium states for an adiabatic systems.

Thermodynamic Stability and Concavity of Entropy¶

• Let us join two systems made of the same substances to make a single system. The entropy maximization principle tells us that the entropy of the resultant compound system is given by

• Where the maximum is taken over all the partitions of $E$ and $X$ (collection of any work coordinates) between the two systems as $E = E_1 + E_2$ and $X = X_1 + X_2$

• This implies with the aid of the extensivity $S(\alpha E, \alpha X) = \alpha S(E, X)$

• for any $\alpha \in [0, 1]$. That is, S is a concave function (its graph is convex upward) of all the thermodynamic coordinates

<img src="./figs/concave_convex.png"  class="bg-primary" width="500px"> 

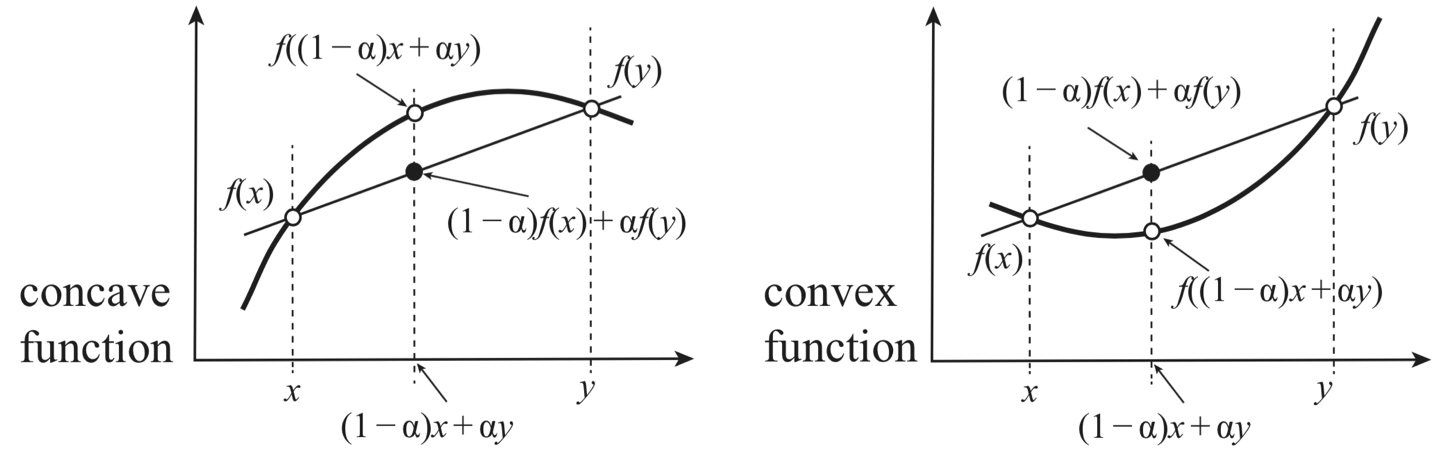
Entropy is a concave function of extensive variables.

Thermodynamic stability and Heat Capacity¶

• The entropy function $S(E, V, N)$ must be concave to ensure stability.

• Mathematically, for equilibrium stability, the second derivative of entropy must satisfy:

• This inequality shows that equilibrium state is stable against any thermal fluctuations that deviate from equilibrium.

• Taking second derivative of entropy and making use of the following equality:

• Since heat capacity at constant volume is:

• we obtain the stability condition:

• Implication: A positive heat capacity ($C_V > 0$) ensures local thermodynamic stability.

Spontaneous Change and Partitioning of Extensive Variables¶

<img src="./figs/part1.png" class="bg-primary" width="300px">  

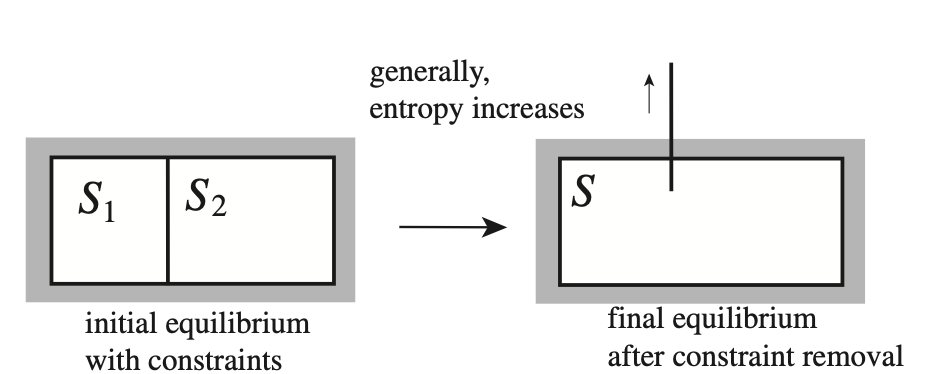
What way the system will parition energy, volume particles when the constraint separating flow of these variables is removed?

• A spontaneous process occurs when a system undergoes a transformation that maximizes entropy. In thermodynamic equilibrium, extensive variables (such as energy, volume, and particle number) partition between subsystems in a way that maximizes the total entropy.

• Consider two subsystems, $I$ and $II$, exchanging energy. Since the total energy is conserved we can write down total energy and entropy as:

  $$E = E_I + E_{II}$$

  (34)
  $$S_{\text{tot}}(E) = S_I(E_I) + S_{II}(E - E_I)$$

  (35)

• At equilibrium, entropy is maximized by varying in this case the only free extensive coordinate $E_I$, which determines energy partitioning:

  $$\delta S_{\text{tot}}(E) = \frac{\partial S_I}{\partial E_I} \delta E_I - \frac{\partial S_{II}}{\partial E_{II}} \delta E_I = 0$$

  (36)
  $$\frac{\partial S_I}{\partial E_I} = \frac{\partial S_{II}}{\partial E_{II}}$$

  (37)

• We once again come to appreciate that derivative of entropy with respect to energy is related to temperature:

  $$\frac{1}{T} = \frac{\partial S}{\partial E}$$

  (38)

  • We obtain the equilibrium condition showing that temperature imbalance drives energy distirbution until we reach equal temperatures throughout the system.

  $$T_I = T_{II}$$

  (39)

• In general system spontaneously evolves toward equilibrium by redistributing energy, volume, and particles:

Appendix¶

Problems¶

Problem 1 Fundamental equations¶

The following ten equations are purported to be fundamental equations for various thermodynamic systems. Five, however, are inconsistent with the basic postulates of a fundamental equation and are thus unphysical. For each, plot the relationship between $S$ and $U$ and identify the unacceptable five. $v_0$, $\theta$, and $R$ are all positive constants and, in the case of fractional exponents, the real positive root is to be implied.

1. $\ S = \left ( \frac{R^2}{v_0\theta} \right )^{1/3}\left ( NVU \right )^{1/3}$

2. $S = \left ( \frac{R}{\theta^2} \right )^{1/3}\left ( \frac{NU}{V} \right)^{2/3}$

3. $S = \left ( \frac{R}{\theta} \right )^{1/2}\left ( NU + \frac{R\theta V^2}{v_0^2} \right)^{1/2}$

4. $S = \left ( \frac{R^2\theta}{v_0^3} \right ) \frac{V^3}{NU}$

5. $S = \left ( \frac{R^3}{v_0\theta^2} \right )^{1/5}\left ( N^2U^2V \right)$

6. $S = NR \ln \left ( \frac{UV}{N^2 R \theta v_0} \right )$

7. $S = \left ( \frac{NRU}{\theta} \right )^{1/2}\exp \left (-\frac{V^2}{2N^2v_0^2} \right )$

8. $S = \left ( \frac{NRU}{\theta} \right )^{1/2}\exp \left (-\frac{UV}{NR\theta v_0} \right )$

9. $U = \left ( \frac{NR\theta V}{v_0} \right ) \left ( 1+\frac{S}{NR} \right ) \exp \left (-S/NR \right)$

10. $U = \left ( \frac{v_0\theta}{R} \right ) \frac{S^2}{V} \exp\left ( S/NR \right)$

Problem 2: Expansion of gas into the vacuum¶

1. As a general case of gas expanding into the vacuum, use the Gibbs relation for $E$ to show that $\Big(\frac{\partial S}{\partial V}\Big)_E>0$ this would show that free adiabatic expansion is accompanied by entropy increase and is hence and irreversible process.

2. Now consider a gas in container energy described by the following equation $E = 3/2NkT −N^2 V/a$

   • Plot E as a function of V for a few temperatures.

   • Suppose that a gas expands adiabatically into a vacuum. How will the energy and entropy of the system change, and what is the work done by the gas?

   • Initially, the gas occupies a volume $V_1$ at a temperature $T_1$. The gas then expands adiabatically into a vacuum to occupy a total volume $V_2$. What is the final temperature $T_2$ of the gas?

Problem 3 Entropy of mixing two gases¶

Using the expression for an ideal gas $S=Nk_B log \frac{V}{N}$, calculate the entropy change resulting after removing a divider separating $N_A$ molecules of gas A occupying Volume $V_A$ from $N_B$ molecules of gas B occupying volume $V_B$.

Hints

• The system overall is thermally insulated and pressure and temperatures are constant; hence, numbers and volumes are proportional $N_A \sim V_A$ so you can express entropy change entirely in terms of molar numbers or their fractions $x_A = N_A/(N_A+N_B)$

• You need to first calculate the entropy change due to gas A expanding from volume $V_A$ to volume $V=V_A+V_B$ and the same for gas B. the total entropy change will be the sum of these two changes.

Problem 4: Entropy of heating¶

1. 1 kg of water (specific heat = 4.2 kJ/(kg·K)) at $0 ^oC$ is in contact with a $50 ^oC$ heat bath, and eventually reaches $50 ^oC$. What is the entropy change of the water? What is the increase of the entropy of this water plus the heat bath?

2. Imagine now that the water at $0 ^oC$ is in contact with a $25 ^oC$ heat bath. Then, after reaching thermal equilibrium, the water is subsequently put in contact with a $50 ^oC$ heat bath until it reaches the final temperature $50 ^oC$. What is the increase of the entropy of the water after it has been put in contact with two heat baths? Compare the answer to the case of (1)

3. Show that in the two-step heating process, whatever the first heat bath temperature T is between $0^oC$ and $50^oC$, the total change of entropy of the water plus heat baths is less than the case of (1)