Summary of Ensembles

Entropy as a Function of Microstate Probabilities¶

Entropy is given by the Shannon-Gibbs entropy formula:

where $p_i$ is the probability of the $i$ th microstate.

Physical Constraints for Equilibrium¶

For a system to maintain equilibrium values, the microstate probabilities must satisfy the following conditions:

1. Normalization:

   $$\sum_{i} p_i = 1$$

   (2)

2. Constraint to Maintain the Expectation Value of an Observable $X$ (e.g., Energy or Volume):

   $$\sum_{i} p_i X_i = \langle X \rangle, \quad \sum_{i} p_i Y_i = \langle Y \rangle$$

   (3)

• The probability of a macrostate $(X, Y, \dots)$ follows the general form:

  $$P(X, Y, \dots) = \frac{e^{\frac{1}{k_B}S(X, Y, ..)} \cdot e^{- \beta X} \cdot e^{- \gamma Y}...}{Z}$$

  (4)
  $$Z(\beta, \gamma, ...) = \sum_{X, Y, ...} e^{\frac{1}{k_B}S(X, Y, ..)} e^{- \beta X} e^{- \gamma Y}...$$

  (5)

• Where $Z$ is a normalization factor called partition function

• Exponential dependence can also be seen as consequence of exchange of (energy, volume ,etc) with an environment or a large reserovoir.

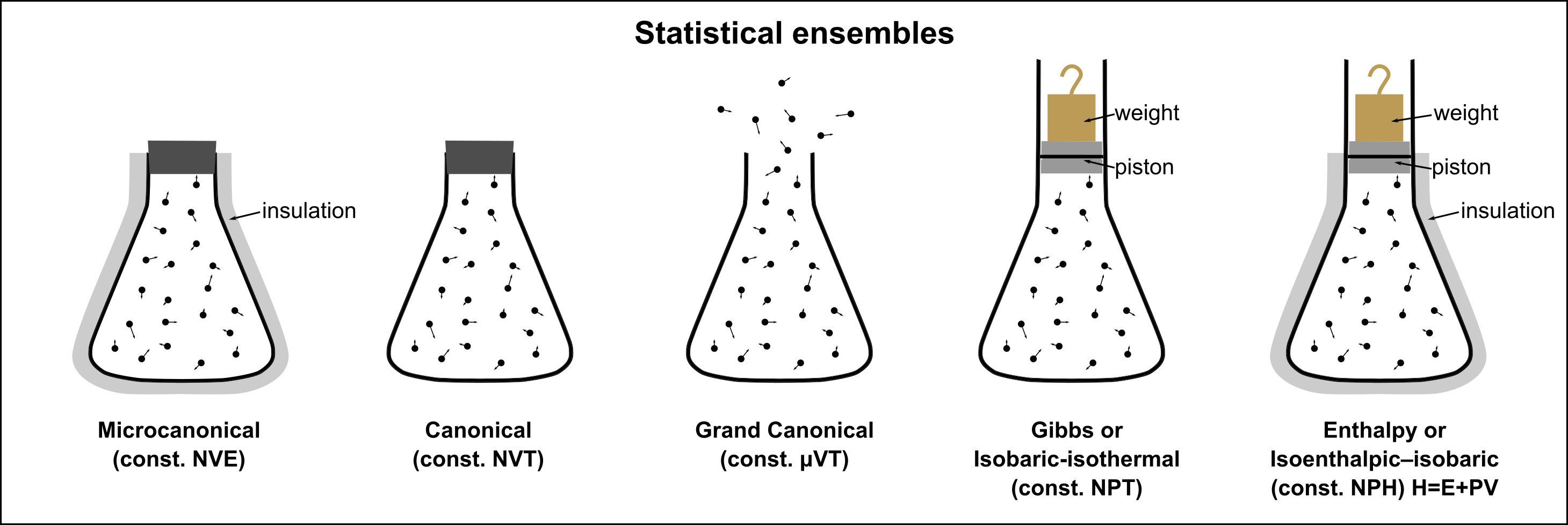
Comparison of Ensembles¶

• Entropy dependence $e^{S/k_B}$ is universal across all ensembles.

• Microstate probability follows different forms based on constraints from different thermodynamic potentials.

• Macrostate probability always includes an entropy term but is modified by energy, pressure, and chemical potential, depending on the ensemble.

Extensive vs intensive variables¶

• The total differential of internal energy $U$ in a thermodynamic system can be expressed in terms of its conjugate variables:

• where each pair $(X_i, f_i)$ represents a conjugate extensive and intensive variable respectively, such as:

  • $(S, T)$ → entropy and temperature,

  • $(V, -P)$ → volume and pressure,

  • $(N, \mu)$ → particle number and chemical potential,

  • $(M, B)$ → magnetization and magnetic field.

Laplace Transform and Ensemble Connections¶

• The Laplace transform connects different thermodynamic ensembles by linking the partition function to energy and volume fluctuations. It effectively approximates a Legendre transform in the thermodynamic limit.

• Canonical Ensemble (Energy Integration):

  $$Z(\beta, N, V) = \int dE \, \Omega(E) e^{-\beta E} \approx e^{\min_E [S(E)/k_B - \beta E]}$$

  (10)
  $$Z(\beta, N, V) = e^{-\beta [U - TS]} = e^{-\beta F(\beta, N, V)}$$

  (11)

• Isothermal-Isobaric Ensemble (Volume Integration):

  $$Z(\beta, N, P) = \int dV \, Z(\beta, N, V) e^{-\beta P V} \approx e^{\min_V [F(V) - \beta P V]}$$

  (12)
  $$Z(\beta, N, P) = e^{-\beta [U - TS - PV]} = e^{-\beta G(\beta, N, P)}$$

  (13)

• Thus, free energy functions naturally emerge as Legendre transforms of internal energy through Laplace integration over fluctuating variables.

Legendre Transform and Thermodynamic Potentials¶

• The Legendre transformation allows us to reformulate equilibrium conditions (e.g., entropy maximization) in terms of more convenient variables (e.g., free energy minimization).

• This transformation makes it possible to work with temperature and pressure as control variables instead of entropy and volume.

• Free Energies as Legendre Transforms of Internal Energy

• Helmholtz Free Energy (Legendre transform over $S$):

• Gibbs Free Energy (Legendre transform over $S, V$):

Partition Functions and Legendre Transforms¶

• The partition function naturally follows the structure of a Legendre transform, as it is related to free energy via:

• The $\Psi$ is a thermodynamic potential obtained through Legendre transformation of the internal energy.

Fluctuation-Response Relations¶

• For a given extensive variable $X$ and its conjugate intensive variable $f$, the partition function $Z$ governs both the mean value and fluctuations of $X$.

• Mean value of $X$ at constant $f$:

  $$\langle X \rangle = \frac{\partial \log Z}{\partial (\beta f)}$$

  (18)

• Fluctuations of $X$ at constant $Y$:

  $$\sigma^2_X = \langle X^2 \rangle - \langle X \rangle^2 = \frac{\partial^2 \log Z}{\partial (\beta f)^2}$$

  (19)

• This relation shows that fluctuations in $X$ are directly linked to the second derivative of the partition function, a fundamental result of statistical mechanics.

Energy fluctuations (Canonical Ensemble):¶

• where $C_V$ is the heat capacity at constant volume.

Particle number fluctuations (Grand Canonical Ensemble):¶

• where $\kappa_T$ is the isothermal compressibility.

Key Insights¶

• Fluctuations decrease as system size increases, typically scaling as $1/\sqrt{N}$.

• Response functions (e.g., heat capacity, compressibility) determine fluctuation magnitude.

• Ensemble equivalence ensures that for large systems, different ensembles (canonical, grand canonical, etc.) give equivalent macroscopic results, despite differing fluctuation magnitudes.