Open Systems

Grand Canonical Ensemble¶

• Consider small system $S$ in thermal and particle exchange with a large reservoir $R$.

• The total system $S + R$ is isolated: total energy $E_{\text{tot}} = E + E_R$, total particle number $N_{\text{tot}} = N + N_R$.

• Total volume is constant, and the reservoir is much larger: $E \ll E_R$, $N \ll N_R$.

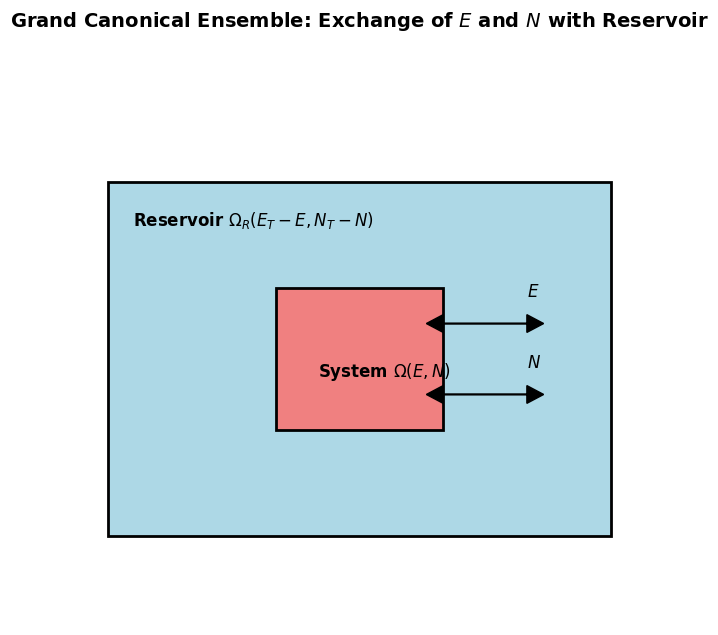
Microstate Probability¶

• The probability that the system has energy $E$ and particle number $N$ is proportional to the number of microstates of the reservoir with $E_R = E_{\text{tot}} - E$, $N_R = N_{\text{tot}} - N$:

• Define entropy of the reservoir $S_R = k_B \ln \Omega_R$. Then:

• Expand to first order:

• Use thermodynamic definitions:

Grand Canonical Distribution and Partition Function¶

Define the grand canonical partition function:

where:

• $z = e^{\beta \mu}$ is called the fugacity.

• $Z_N = \sum_{\text{states at fixed } N} e^{-\beta E}$ is the canonical partition function at fixed $N$

• The microstate probability in grand canonical ensemble is:

• The macrostate probability over different energy values in grand canonical ensemble is:

Connections with $NVE$ and $NVT$¶

Statistical Dominance of Average Energy and Particle Number¶

• Recall that the canonical ensemble emerges by weighting microcanonical contributions at different energies with an exponential factor $e^{-\beta E}$.

• Similarly, the grand canonical ensemble arises by further summing over all particle numbers $N$, each weighted by the fugacity factor $e^{\beta \mu N}$. This yields the grand canonical partition function:

  $$\Xi(T, V, \mu) = \sum_{N=0}^{\infty} \left[ \sum_i e^{-\beta E_i} \right] e^{\beta \mu N} = \sum_{N=0}^{\infty} Z(N, V, T) \, e^{\beta \mu N}$$

  (12)

• In the thermodynamic limit, the sum is dominated by the most probable energy and particle number, giving:

  $$\Xi \approx e^{-\beta (F - \mu \bar{N})} = e^{-\beta (\bar{E} - T S - \mu \bar{N})} = e^{-\beta \Psi(T, V, \mu)}$$

  (13)

• We identify a new thermodynamic potential for the grand canonical ensemble that plays same role as free energy in canonical ensemble:

Thermodynamics and Legendre transform¶

• In thermodynamics grand potential $\Psi$ is derived from the internal energy $E(S, V, N)$ via a Legendre transform that replaces the natural variables $S \to T$ and $N \to \mu$:

  $$E(S, V, N) \rightarrow E - \left( \frac{\partial E}{\partial S} \right) S - \left( \frac{\partial E}{\partial N} \right) N = E - T S - \mu N$$

  (15)

Grand Potential and Pressure¶

• Using Euler’s relation for extensive thermodynamic variables:

  $$E = T S + P V + \mu N$$

  (16)

• Substituting into the definition of $\Psi$, we find:

  $$\Psi = E - T S - \mu N = -P V$$

  (17)

• Hence, the grand potential is directly related to the pressure and volume:

  $${\Psi(T, V, \mu) = -P V}$$

  (18)

Fluctuations in particle numbers¶

• We once again find that in case of fluctuating quantities (energy in NVT) the relative fluctuation scales as $N^{-1/2}$ a hallmark of Central Limit Theorem!

• Using thermodynamics we could also link number fluctuations with isothermal compressibility $\kappa_T$

• The relationship is analogus to what we had established in $NVT$ between energy flcutuations and heat capcity.

• It takes a bit more work manipulating variables to get there in this case. See belwo for derivation:

Ideal Gas in the Grand Canonical Ensemble¶

• We begin by considering an ideal gas of indistinguishable, non-interacting particles in a volume $V$, in thermal and chemical equilibrium with a reservoir at temperature $T$ and chemical potential $\mu$.

• The canonical partition function for $N$ particles is:

• Where the thermal de Broglie wavelength is:

Grand Canonical Partition Function¶

• To account for fluctuations in particle number, we compute the grand canonical partition function:

• Fugacity: $z = e^{\beta \mu}$, a dimensionless measure of how favorable it is to add a particle to the system.

• The average particle number is then obtained by taking first derivative withr espect to N

Chemical Potential in Terms of Pressure and Density¶

• We can invert the relation for $\langle N \rangle$ to express the chemical potential:

• Noting that for an ideal gas $p = \frac{N k_B T}{V}$, this becomes:

Number Fluctuations¶

• In the grand canonical ensemble, number fluctuations are given by:

• So the standard deviation $\sigma_N \sim \sqrt{N}$, and relative fluctuations vanish as $N^{-1/2}$ in the thermodynamic limit.

Isothermal Compressibility¶

• We relate number fluctuations to the isothermal compressibility $\kappa_T$:

• This is the well-known result for the ideal gas compressibility:

• $\kappa_T = \frac{1}{p} \geq 0$, a positive quantity ensuring mechanical stability.

Molecular Adsorption of Ideal Gas on Surfaces¶

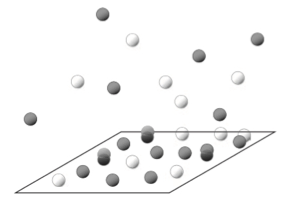
One Site–One Molecule Model¶

We consider a simple model where each adsorption site can hold at most one molecule. The surface is in thermal and chemical equilibrium with a gas reservoir at temperature $T$ and chemical potential $\mu$.

• Each site has two possible states:

  • Empty: energy $E = 0$

  • Occupied: energy $E = \epsilon$

• Then the grand partition function for a single site is:

$N$ Independent Sites¶

• If there are $N$ independent and identical adsorption sites, then the total grand partition function is:

• Since the sites do not interact, their contributions multiply.

Average Number of Adsorbed Molecules¶

The average occupation number per site is:

The total number of adsorbed molecules is:

Average Energy¶

The average energy per site is:

The total energy of the system is:

Connecting to Pressure¶

• For an ideal gas in the reservoir, the chemical potential is related to pressure via:

• Substituting this into the expression for $\langle n \rangle$:

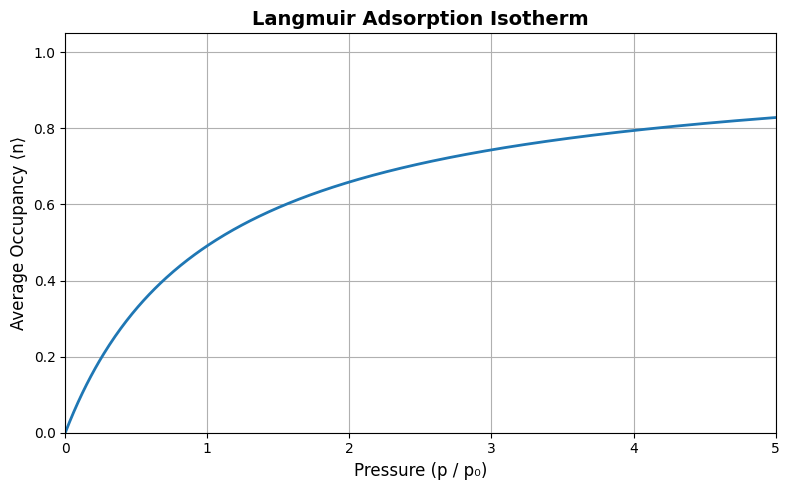
• and thus the total number of adsorbed molecules becomes:

• This is the Langmuir adsorption isotherm, describing how the fraction of occupied adsorption sites depends on gas pressure. It captures saturation behavior as $p \to \infty$, where $\langle n \rangle \to 1$.

Chemical Equilibrium in gas mixtures¶

For each species $i$, the canonical partition function is:

where:

• $\lambda_i = \frac{h}{\sqrt{2\pi m_i k_B T}}$ is the thermal wavelength,

• $q_i^{\text{int}}$ is the internal partition function (rotations, vibrations, etc.),

• $N_i$ is the number of molecules of species $i$.

• For conenvience lets use the Helmholtz free energy (same result with Gibbs Free energy):

• Using Stirling’s approximation $\log N_i! \approx N_i \log N_i - N_i$:

Equilibrium via minimization of free energy¶

• Now, we consider a chemical reaction:

• We introduce an extent of reaction $\xi$ which measures how far reaction has progressed from reactants to products:

• We minimize $F(\xi)$ at constant $T, V$ by setting:

• Computing the derivative:

• with $\nu_i$ the stoichiometric coefficient ($< 0$ for reactants, $> 0$ for products). Or we can write it in terms of positive stochimoetric coefficients:

• So the equilibrium condition is:

• Exponentiating both sides we relate ration of equilibrium numbers or concentrations to partition functions

Problems¶

$NVT-NVE-\mu V T$¶

1. Consider a three level single particle system with five microstates with energies 0, ε, ε, ε, and 2ε. What is $\Omega(\epsilon n)$ n=0,1,2 for this system? What is the mean energy of the system if is in equilibrium with a heat bath at temperature T ?

2. Derive an expression for the chemical potential of an ideal gas using clssical mechanics model for energy $E=\frac{p^2}{2m}$ in the $\mu VT$ ensemble evaluate the fluctuations in particle number.

3. Consider a system in equilibrium with a heat bath at temperature $T$ and a particle reservoir at chemical potential $\mu$. The system can have a minimum of one and a maximum of four distinguishable particles. The particles in the system do not interact and can be in one of two states with energies zero or $\Delta$. Determine the (grand) partition function of the system.

4. Combine the Gibbs formula of Entropy $S=-k_B \sum_i p_i log p_i$ with the Grand canonical prbability distribution $P(E_i,N)=\frac{e^{-\beta E_i+ \beta \mu N}}{Z_G}$ to show that $\beta PV=log Z_G$

5. Derive partition function for a pressure ensemble $(T, p, N)$ and show its connection with microcanonical ensemble $N V E$

6. At a given temperature T a surface with $N_0$ adsorption centers has on average $N\neq N_0$ number of adsorbed molecules. Suppose hat there are no interactions between molecules.

   • Show that the chemical potential of adsorbed gas is given by: $\mu = k_B T log \frac{N}{N_0 - N a(T)}$

   • What is the meaning of $a(T)$