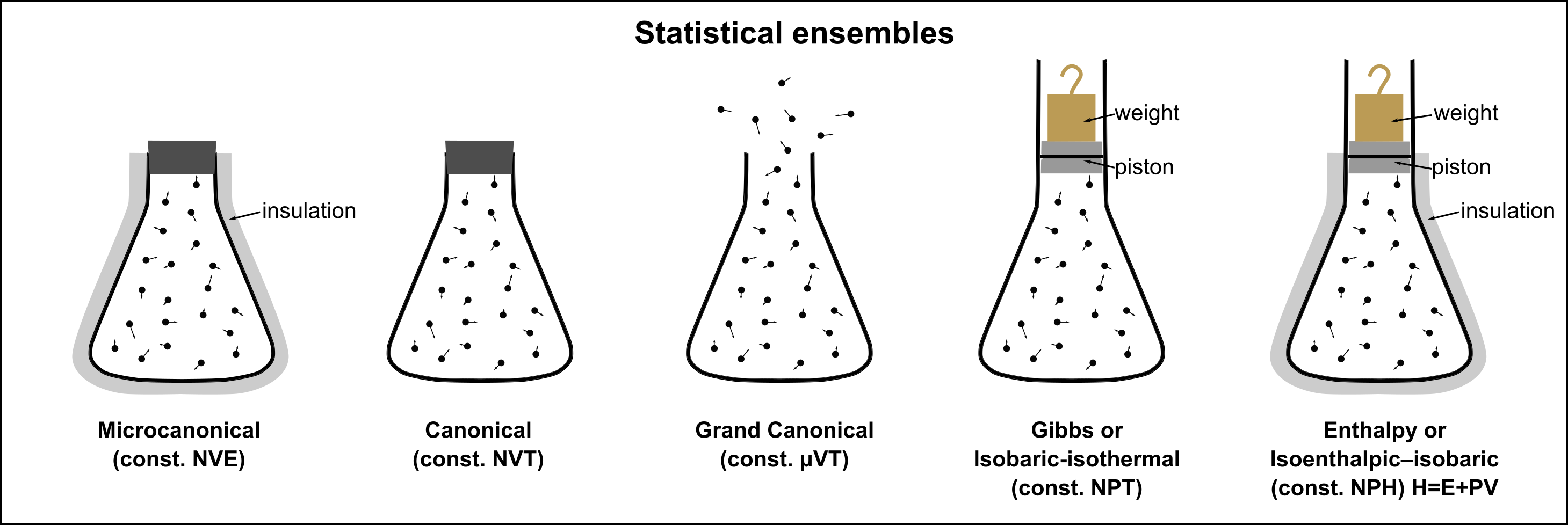
Summary of Ensembles#

Entropy as a Function of Microstate Probabilities#

Entropy is given by the Shannon-Gibbs entropy formula:

\[ S([p]) = -k_B \sum_{i} p_i \log p_i \]

where \(p_i\) is the probability of the \(i\) th microstate.

Physical Constraints for Equilibrium#

For a system to maintain equilibrium values, the microstate probabilities must satisfy the following conditions:

  1. Normalization:

    \[ \sum_{i} p_i = 1 \]

  2. Constraint to Maintain the Expectation Value of an Observable \(X\) (e.g., Energy or Volume):

    \[ \sum_{i} p_i X_i = \langle X \rangle, \quad \sum_{i} p_i Y_i = \langle Y \rangle \]

  • The probability of a macrostate \( (X, Y, \dots) \) follows the general form:

    \[ P(X, Y, \dots) = \frac{e^{\frac{1}{k_B}S(X, Y, ..)} \cdot e^{- \beta X} \cdot e^{- \gamma Y}...}{Z} \]
    \[Z(\beta, \gamma, ...) = \sum_{X, Y, ...} e^{\frac{1}{k_B}S(X, Y, ..)} e^{- \beta X} e^{- \gamma Y}...\]

  • Where \(Z\) is a normalization factor called partition function

  • Exponential dependence can also be seen as consequence of exchange of (energy, volume ,etc) with an environment or a large reserovoir.

\[E_r\gg E,\quad V_r \gg V, \quad N_t \gg N\]
\[log \Omega_r(E_t-E, V_r-V, N_r-N,)\approx const - \beta E + \beta\mu -\beta PV \]
\[P(E, N, V) \sim \Omega \cdot \Omega_r \sim e^{S(E, N, V)} \cdot e^{-\beta E} \cdot e^{\beta \mu N} \cdot e^{-\beta PV} \]

Comparison of Ensembles#

Ensemble

\( P(\text{microstate}) \)

\( P(\text{macrostate}) \)

Microcanonical (NVE)

\( P(\text{microstate}) = \frac{1}{\Omega(E)} \)

\( P(E) \sim e^{S(E)/k_B} \) (entropy-dominated)

Canonical (NVT)

\( P(\text{microstate}) \sim e^{-\beta E} \)

\( P(E) \sim e^{S(E)/k_B - \beta E} \) (entropy-weighted by energy)

Grand Canonical (µVT)

\( P(\text{microstate}) \sim e^{\beta (\mu N - E)} \)

\( P(N, E) \sim e^{S(N,E)/k_B + \beta (\mu N - E)} \)

Isothermal-Isobaric (NPT)

\( P(\text{microstate}) \sim e^{-\beta (E + PV)} \)

\( P(E, V) \sim e^{S(E, V)/k_B - \beta (E + PV)} \)

  • Entropy dependence \(e^{S/k_B}\) is universal across all ensembles.

  • Microstate probability follows different forms based on constraints from different thermodynamic potentials.

  • Macrostate probability always includes an entropy term but is modified by energy, pressure, and chemical potential, depending on the ensemble.

Extensive vs intensive variables#

  • The total differential of internal energy \( U \) in a thermodynamic system can be expressed in terms of its conjugate variables:

\[ dU = TdS-pdV + \mu dN + BdM + \dots = \sum_i f_i dX_i \]

  • where each pair \((X_i, f_i)\) represents a conjugate extensive and intensive variable respectively, such as:

    • \( (S, T) \) → entropy and temperature,

    • \( (V, -P) \) → volume and pressure,

    • \( (N, \mu) \) → particle number and chemical potential,

    • \( (M, B) \) → magnetization and magnetic field.

Laplace Transform and Ensemble Connections#

  • The Laplace transform connects different thermodynamic ensembles by linking the partition function to energy and volume fluctuations. It effectively approximates a Legendre transform in the thermodynamic limit.

  • Canonical Ensemble (Energy Integration):

    \[ Z(\beta, N, V) = \int dE \, \Omega(E) e^{-\beta E} \approx e^{\min_E [S(E)/k_B - \beta E]} \]
    \[ Z(\beta, N, V) = e^{-\beta [U - TS]} = e^{-\beta F(\beta, N, V)} \]

  • Isothermal-Isobaric Ensemble (Volume Integration):

    \[ Z(\beta, N, P) = \int dV \, Z(\beta, N, V) e^{-\beta P V} \approx e^{\min_V [F(V) - \beta P V]} \]
    \[ Z(\beta, N, P) = e^{-\beta [U - TS - PV]} = e^{-\beta G(\beta, N, P)} \]

  • Thus, free energy functions naturally emerge as Legendre transforms of internal energy through Laplace integration over fluctuating variables.

Legendre Transform and Thermodynamic Potentials#

  • The Legendre transformation allows us to reformulate equilibrium conditions (e.g., entropy maximization) in terms of more convenient variables (e.g., free energy minimization).

  • This transformation makes it possible to work with temperature and pressure as control variables instead of entropy and volume.

  • Free Energies as Legendre Transforms of Internal Energy

  • Helmholtz Free Energy (Legendre transform over \( S \)):

\[F(N, V, T) = U - T S = \mathcal{L}_{S} U(S, V, N)\]

  • Gibbs Free Energy (Legendre transform over \( S, V \)):

\[G(N, P, T) = U - T S + P V = \mathcal{L}_{S, V} U(S, V, N)\]

Partition Functions and Legendre Transforms#

  • The partition function naturally follows the structure of a Legendre transform, as it is related to free energy via:

\[ \Psi(f_1, \dots, f_{n}, X_{n+1}, \dots, X_{N}) = U(X_1, ... X_N) - (f_1 X_1+...f_nX_n) \]
\[ Z(f_1, \dots, f_n, X_{n+1}, \dots, X_N) = e^{-\beta \Psi(f_1, \dots, f_{n}, X_{n+1}, \dots, X_{N})} \]

  • The \(\Psi\) is a thermodynamic potential obtained through Legendre transformation of the internal energy.

Fluctuation-Response Relations#

  • For a given extensive variable \( X \) and its conjugate intensive variable \( f \), the partition function \( Z \) governs both the mean value and fluctuations of \( X \).

  • Mean value of \( X \) at constant \( f \):

    \[ \langle X \rangle = \frac{\partial \log Z}{\partial (\beta f)} \]

  • Fluctuations of \( X \) at constant \( Y \):

    \[ \sigma^2_X = \langle X^2 \rangle - \langle X \rangle^2 = \frac{\partial^2 \log Z}{\partial (\beta f)^2} \]

  • This relation shows that fluctuations in \( X \) are directly linked to the second derivative of the partition function, a fundamental result of statistical mechanics.

Energy fluctuations (Canonical Ensemble):#

\[ \sigma^2_E = k_B T^2 C_V \]

  • where \( C_V \) is the heat capacity at constant volume.

Particle number fluctuations (Grand Canonical Ensemble):#

\[ \sigma^2_N = k_B T \frac{\kappa_T}{V} \]

  • where \( \kappa_T \) is the isothermal compressibility.

Key Insights#

  • Fluctuations decrease as system size increases, typically scaling as \(1/\sqrt{N}\).

  • Response functions (e.g., heat capacity, compressibility) determine fluctuation magnitude.

  • Ensemble equivalence ensures that for large systems, different ensembles (canonical, grand canonical, etc.) give equivalent macroscopic results, despite differing fluctuation magnitudes.