MD/MC simulations of fluids#
What you will learn
Molecular dynamics: Solve Newton’s equations of motion for many particles.
Velocity Verlet algorithm: A symplectic, time-reversible integration method.
Periodic boundary conditions: Simulate a small part of a bulk system.
Minimum image convention: Correct distance calculation across periodic boundaries.
Lennard-Jones fluid: Standard model for simple liquids.
Temperature control: Via velocity rescaling.
Structural analysis: Computation of the radial distribution function \(g(r)\).
Molecular Dynamics Simulation of a Lennard-Jones Fluid#
The code in this notebook simulates a collection of particles interacting through the Lennard-Jones (LJ) potential using Molecular Dynamics (MD) in 3D.
The simulation is designed to be efficient, modular, and easy to understand, leveraging NumPy and object-oriented programming (OOP).Particles are initially arranged in a face-centered cubic (FCC) lattice and evolved over time using the Velocity Verlet algorithm under periodic boundary conditions.
The simulation tracks: Kinetic Energy (KE), Potential Energy (PE), Pressure, Pair correlation function \(g(r)\)
Physical Model of LJ fluid#
Each particle experiences a force given by the Lennard-Jones potential:
\(r\) is the distance between two particles.
The potential is cut off at a radius (r_c) to improve efficiency.
The system is simulated at a fixed temperature by rescaling velocities during the early steps (velocity rescaling).
PBC#
If a particle leaves the box, it re-enters at the opposite side.
What should be the distance between partiles? There is some mbiguity because distance between atoms may now include crossing the system boundary and re-entering. This is identical to introducing copies of the particles around the simulation box. We adopt minimum image convention by choosing the shortest distance possible
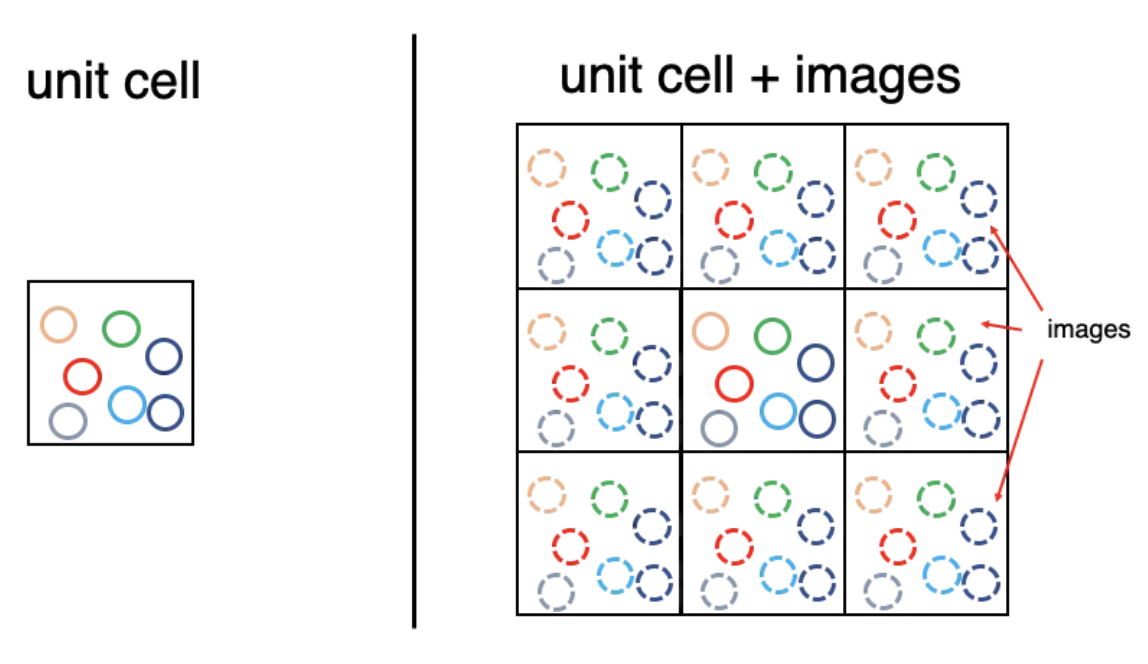
Fig. 32 Perioidc Boundary Conditions#
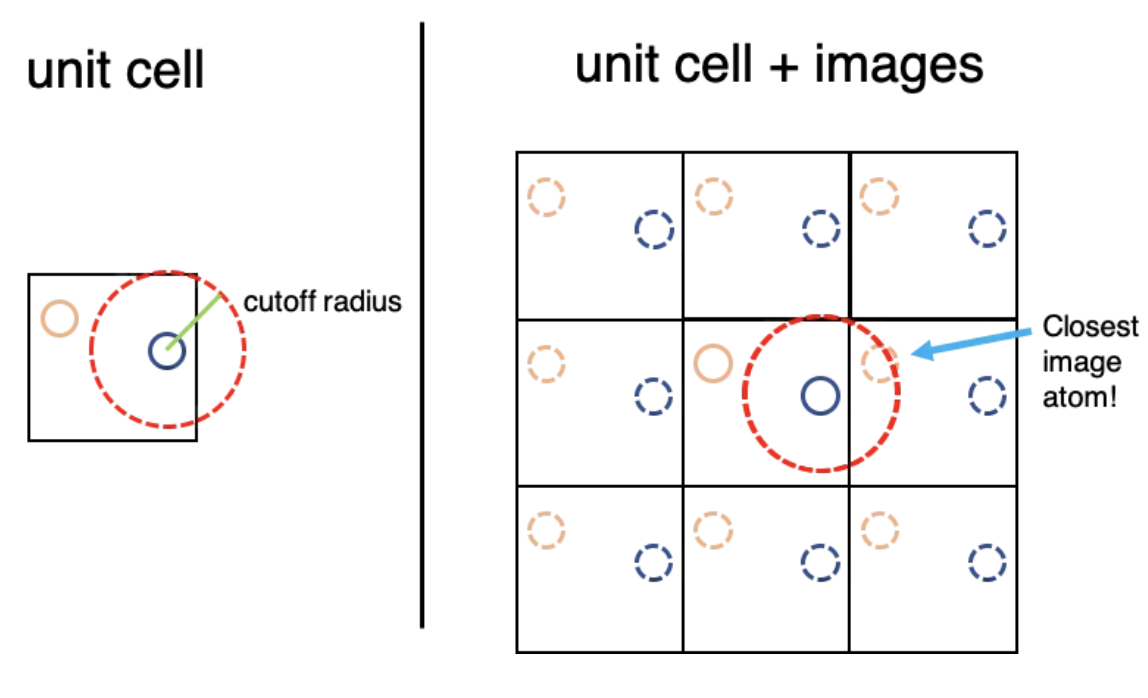
Fig. 33 Minimum Image Convention showing that we only track particles with clsoest distance.#
MD of LJ fluid#
Velocity Verlet Algorithm
1. Evaluate the initial force from the current position:
2. Update the position:
3. Partially update the velocity:
4. Evaluate the force at the new position:
5. Complete the velocity update:
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
class LJSystem:
def __init__(self, rho=0.88, N_cell=3, T=1.0, rcut=2.5):
# System parameters
self.N = 4 * N_cell**3
self.rho = rho
self.L = (self.N / rho)**(1/3)
self.T_target = T
self.rcut = rcut
self.rcut_sq = rcut**2
# Create FCC lattice positions
base = np.array([[0, 0, 0], [0.5, 0.5, 0], [0.5, 0, 0.5], [0, 0.5, 0.5]])
pos = np.array([b + [i, j, k] for i in range(N_cell) for j in range(N_cell) for k in range(N_cell) for b in base])
self.pos = pos * (self.L / N_cell)
# Velocities
self.vel = np.random.randn(self.N, 3)
self.vel -= np.mean(self.vel, axis=0)
# Indices for upper triangular part
self.I, self.J = np.triu_indices(self.N, k=1)
def minimum_image(self, r_vec):
return (r_vec + self.L/2) % self.L - self.L/2
def compute_forces(self):
r_vec = self.minimum_image(self.pos[self.I] - self.pos[self.J])
r_sq = np.sum(r_vec**2, axis=1)
mask = r_sq < self.rcut_sq
r_vec = r_vec[mask]
r_sq = r_sq[mask]
r2_inv = 1.0 / r_sq
r6_inv = r2_inv**3
dU_dr = 48 * r6_inv * (r6_inv - 0.5) * r2_inv
F_ij = dU_dr[:, None] * r_vec
# Forces on each particle
forces = np.zeros_like(self.pos)
np.add.at(forces, self.I[mask], F_ij)
np.add.at(forces, self.J[mask], -F_ij)
# Potential energy
U = 4 * np.sum(r6_inv * (r6_inv - 1))
# Virial for pressure
Pvir = np.sum(np.sum(F_ij * r_vec, axis=1))
# Histogram for g(r)
hist, _ = np.histogram(np.sqrt(r_sq), bins=30, range=(0, self.L/2))
return forces, U, Pvir, hist
def integrate(self, dt):
forces, U, Pvir, hist = self.compute_forces()
self.vel += 0.5 * dt * forces
self.pos = (self.pos + dt * self.vel) % self.L
forces_new, U_new, Pvir_new, hist_new = self.compute_forces()
self.vel += 0.5 * dt * forces_new
kin = 0.5 * np.sum(self.vel**2)
return kin, U_new, Pvir_new, hist_new
def rescale_velocities(self, kin):
"""Velocity rescaling to maintain target temperature"""
factor = np.sqrt(3 * self.N * self.T_target / (2 * kin))
self.vel *= factor
def simulate(self, dt=0.005, nsteps=5000, freq_out=50):
kins, pots, Ps, hists = [], [], [], []
for step in range(nsteps):
kin, pot, Pvir, hist = self.integrate(dt)
if step < 1000: # Temperature stabilization
self.rescale_velocities(kin)
if step % freq_out == 0:
kins.append(kin)
pots.append(pot)
Ps.append(Pvir)
hists.append(hist)
return np.array(kins), np.array(pots), np.array(Ps), np.mean(hists, axis=0)
Example simulation and analysis#
# Initialize system
lj = LJSystem(rho=0.88, N_cell=3, T=1.0)
# Run simulation
kins, pots, Ps, hist = lj.simulate(dt=0.005, nsteps=10000, freq_out=50)
# Post-processing
r = np.linspace(0, lj.L/2, 30)
dr = r[1] - r[0]
shell_volumes = 4*np.pi*r**2*dr
g_r = hist / (lj.N * lj.rho * shell_volumes)
# Plot
plt.plot(r, g_r, '-o')
plt.xlabel(r'$r$')
plt.ylabel(r'$g(r)$')
plt.show()
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Cell In[2], line 5
2 lj = LJSystem(rho=0.88, N_cell=3, T=1.0)
4 # Run simulation
----> 5 kins, pots, Ps, hist = lj.simulate(dt=0.005, nsteps=10000, freq_out=50)
7 # Post-processing
8 r = np.linspace(0, lj.L/2, 30)
Cell In[1], line 76, in LJSystem.simulate(self, dt, nsteps, freq_out)
74 kins, pots, Ps, hists = [], [], [], []
75 for step in range(nsteps):
---> 76 kin, pot, Pvir, hist = self.integrate(dt)
78 if step < 1000: # Temperature stabilization
79 self.rescale_velocities(kin)
Cell In[1], line 63, in LJSystem.integrate(self, dt)
61 self.vel += 0.5 * dt * forces
62 self.pos = (self.pos + dt * self.vel) % self.L
---> 63 forces_new, U_new, Pvir_new, hist_new = self.compute_forces()
64 self.vel += 0.5 * dt * forces_new
65 kin = 0.5 * np.sum(self.vel**2)
Cell In[1], line 34, in LJSystem.compute_forces(self)
31 r_sq = np.sum(r_vec**2, axis=1)
33 mask = r_sq < self.rcut_sq
---> 34 r_vec = r_vec[mask]
35 r_sq = r_sq[mask]
37 r2_inv = 1.0 / r_sq
KeyboardInterrupt:
MC simulation#
MCMC of LJ fluid
Randomly pick a particle.
Propose a random displacement.
Compute the change in energy \(\Delta E\).
Accept or reject the move based on the Metropolis criterion:
If the move is rejected, the particle returns to its previous position.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
class LJ_MC_System:
def __init__(self, rho=0.88, N_cell=3, T=1.0, rcut=2.5):
# System parameters
self.N = 4 * N_cell**3
self.rho = rho
self.L = (self.N / rho)**(1/3)
self.T = T
self.beta = 1.0 / T
self.rcut = rcut
self.rcut_sq = rcut**2
# Create FCC lattice positions
base = np.array([[0, 0, 0], [0.5, 0.5, 0], [0.5, 0, 0.5], [0, 0.5, 0.5]])
pos = np.array([b + [i, j, k] for i in range(N_cell) for j in range(N_cell) for k in range(N_cell) for b in base])
self.pos = pos * (self.L / N_cell)
# Pair indices
self.I, self.J = np.triu_indices(self.N, k=1)
def minimum_image(self, r_vec):
return (r_vec + self.L/2) % self.L - self.L/2
def total_energy(self):
r_vec = self.minimum_image(self.pos[self.I] - self.pos[self.J])
r_sq = np.sum(r_vec**2, axis=1)
mask = r_sq < self.rcut_sq
r2_inv = 1.0 / r_sq[mask]
r6_inv = r2_inv**3
return 4 * np.sum(r6_inv * (r6_inv - 1))
def particle_energy(self, idx):
rij = self.minimum_image(self.pos[idx] - self.pos)
r_sq = np.sum(rij**2, axis=1)
mask = (r_sq < self.rcut_sq) & (r_sq > 0) # exclude self-interaction
r2_inv = 1.0 / r_sq[mask]
r6_inv = r2_inv**3
return 4 * np.sum(r6_inv * (r6_inv - 1))
def mc_move(self, max_disp=0.1):
idx = np.random.randint(self.N)
old_pos = self.pos[idx].copy()
old_energy = self.particle_energy(idx)
# Propose move
displacement = (np.random.rand(3) - 0.5) * 2 * max_disp
self.pos[idx] = (self.pos[idx] + displacement) % self.L
new_energy = self.particle_energy(idx)
dE = new_energy - old_energy
# Metropolis criterion
if np.random.rand() > np.exp(-self.beta * dE):
# Reject move
self.pos[idx] = old_pos
def sample(self):
""" Sample pair distances for g(r) """
r_vec = self.minimum_image(self.pos[self.I] - self.pos[self.J])
r_sq = np.sum(r_vec**2, axis=1)
hist, _ = np.histogram(np.sqrt(r_sq), bins=30, range=(0, self.L/2))
return hist
def simulate(self, nsteps=50000, freq_out=500):
hists = []
energies = []
for step in range(nsteps):
self.mc_move()
if step % freq_out == 0:
hist = self.sample()
hists.append(hist)
energies.append(self.total_energy())
return np.array(energies), np.mean(hists, axis=0)
Example MC simulation and analysis#
# ----------------- Main -----------------
# Initialize system
lj_mc = LJ_MC_System(rho=0.88, N_cell=3, T=1.0)
# Run simulation
energies, hist = lj_mc.simulate(nsteps=100000, freq_out=500)
# Post-processing
r = np.linspace(0, lj_mc.L/2, 30)
dr = r[1] - r[0]
shell_volumes = 4*np.pi*r**2*dr
g_r = hist / (lj_mc.N * lj_mc.rho * shell_volumes)
# Plot
plt.plot(r, g_r, '-o')
plt.xlabel(r'$r$')
plt.ylabel(r'$g(r)$')
plt.show()
Differences of Monte Carlo vs Molecular Dynamics#
Monte Carlo (MC) |
Molecular Dynamics (MD) |
|---|---|
No real dynamics, just configurations |
Real-time evolution of particle trajectories |
Samples equilibrium ensemble directly |
Samples via time evolution |
No conservation laws |
Energy/momentum conserved after equilibration |
Easier to implement |
More complex (forces, integration needed) |
Faster for static properties like \(g(r)\) |
Necessary for dynamics (diffusion, viscosity) |
Problems#
MD sim of LJ fluid#
Modify the cut-off radius \(r_c\) and observe its effect on pressure and energy.
Remove velocity rescaling after equilibration and check energy conservation.
Implement a thermostat (e.g., Andersen, Berendsen) instead of manual rescaling.
Compute the diffusion coefficient from particle trajectories.
Visualize the particle trajectories over time (animation!).
MC sim of LJ fluid#
Vary sim parameters
Tune maximum displacement (
max_disp) to optimize acceptance rate (~40%-50% is ideal).Check how \(g(r)\) changes when density or temperature changes.
Implement energy cutoffs with shifted potentials to smooth out the energy at \(r_c\).
Try simulating hard spheres (infinite repulsion at contact).
Phases of LJ fluid#
Run MD or MC simulations of LJ fluid at several temperatures to identify critical temperature.
At each temperature evaluate heat capacity and RDFs.
Plot how energy, heat capacity and RDF change as a function of temperature.
Study dependence on sampling efficiency on magnitude of particle displacement.


