The Inverse Transform of RVs#

%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

The idea#

  • Inverse transform sampling is a basic method for pseudo-random number sampling, i.e. for generating sample numbers at random from any probability distribution given its cumulative distribution function. That is, by drawing from a uniform distribution, we make it possible to draw from the other distribution in question.

  • Let’s start by defining uniform distribution \(U(0,1)\) which generates random numbers \(Z\sim U(0,1)\) falling on \([0,1]\) range. Now let’s look for a way of transforming random number \(Z\) with \(p(z)=\frac{1}{1-0}\) uniform pdf into a function \(X(Z)\) where x is distributed according to some pdf \(p(x)\). The probability to find \(x\) between \(x\) and \(x+dx\) is equal to:

\[p(x)dx = p(z)dz = dz\]

  • This relation is simply transform of variables. Now the key point to realize is that integrals from over \([-\infty, x(z)]\) for X and \([0, z]\) for Z are equal (these are cumulative distribution functions (CDF).

\[ \int_{-\infty}^{x(z)} p(x') dx' = \int_0^z dz'= z \]

  • Thus, if we can (i) integrate expression on the left analytically and (ii) solve for \(x\) then we are done! For most of the pdf at least one of the two is not possible. Below is a typical example where both (i) and (ii) states are easily done.

Example: Drawing from the exponential distribution.#

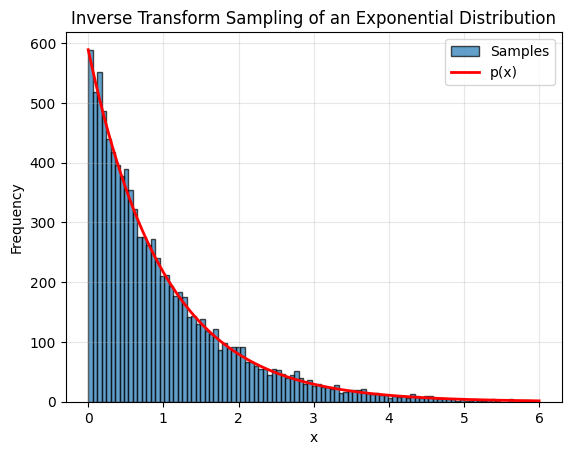
  • For example, lets assume we would like to generate random numbers that follow the exponential distribution $\(p(x) = \frac{1}{\lambda} e^{-x/\lambda}\)$

  • for \(x\ge0\) and \(f(x)=0\) otherwise. Following the recipe from the above we have

\[u = \int_{0}^{x} \frac{1}{\lambda} e^{-x'/\lambda} dx' = 1- e^{-x/\lambda} \]

  • Solving for \(x\) we get

\[x = - \lambda \ln (1-u) \]

Formalized procedure:#

  1. Get a uniform sample \(u\) from \(U(0,1)\)

  2. Solve for \(x\) yielding a new equation \(x=F^{-1}(u)\) where \(F\) is the CDF of the distribution we desire.

  3. Repeat.

# Define the probability distribution function
p = lambda x: np.exp(-x)

# Compute its cumulative distribution function (CDF)
CDF = lambda x: 1 - np.exp(-x)

# Compute the inverse of the CDF
invCDF = lambda r: -np.log(1 - r)

# Define sampling limits
xmin, xmax = 0, 6  # Domain range
rmin, rmax = CDF(xmin), CDF(xmax)  # Range of CDF values

# Generate random samples
N = 10000
R = np.random.uniform(rmin, rmax, N)
X = invCDF(R)

# Compute histogram data
hist_vals, bin_edges = np.histogram(X, bins=100)

# Plot histogram of samples
plt.hist(X, bins=100, label='Samples', alpha=0.7, edgecolor='black')

# Overlay the theoretical probability density function (PDF)
x_vals = np.linspace(xmin, xmax, 1000)
plt.plot(x_vals, hist_vals[0] * p(x_vals), 'r', linewidth=2, label='p(x)')

# Display legend and formatting
plt.legend()
plt.xlabel('x')
plt.ylabel('Frequency')
plt.title('Inverse Transform Sampling of an Exponential Distribution')
plt.grid(alpha=0.3)
plt.show()
../../_images/acdb3f74e952dbce2da94e832ee91a8169c24c3b956e32e71c39c4432865b573.png