Photoelectric effect#
What You Will Learn.
Photoelectric Effect: Electrons are ejected from the surface of a material when it is exposed to radiation with a frequency exceeding a specific threshold frequency.
Threshold Frequency: No electrons are ejected if the radiation’s frequency is below this threshold, regardless of the light’s intensity (brightness).
Classical vs. Quantum The photoelectric effect cannot be explained using classical mechanics, where energy is thought to increase continuously with light intensity. However, in quantum mechanics, energy is quantized. Radiation is treated as a stream of photons, which are discrete packets of energy.
Photon-Electron Interaction: A single photon can eject a single electron if the photon has sufficient energy. Any excess energy is converted into the kinetic energy of the ejected electron, causing it to move faster.
Insufficient Energy: Photons with energy below the threshold will not eject electrons; instead, they scatter off the material.
High-Intensity Light: Even high-intensity light, which means more photons per unit area per unit time, cannot eject electrons if the photons lack sufficient energy.
Photoelectric effect challanges classical mechanical thinking.#
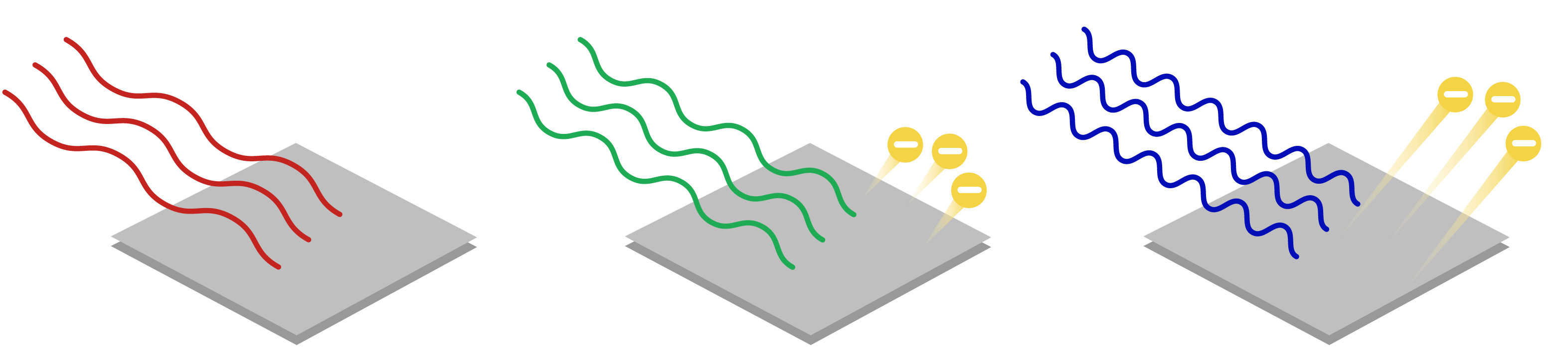
Fig. 16 Shown are different effects of radiation on material depending on frequency. From left to right frequency of radiation is increasing.#
When you shine a radiation on a metal surface after a some threshold frequency electrons will start flying off the surface.
Below this frequency no electrons are not ejected regardless of the intensity of radiation.
This experiment challanged classical way of thinking about radiation according to which energy of radiation is proportional to amplitude of wave which is its intensity or brightness of the light.
Introducing Photon#
Recall that to reconcile experiment with theory Planck was already forced to introduce quantization of black bodies modleed as spings that can only assume discrete energies: \(0, h\nu, 2h\nu, 3h\nu, …\) giving off radiation with same frequencies!
At that time this discreteness introduced by Placnk was thought to be nothing more than a temporary mathematical trick to fit experimental curve.
Einstein, on the other hand, was more imaginative and saw in Plank’s prescription more than just a math trick. He suggested that light can behave like a stream of particles with discrete countable energy packets which he called photons. This view was instrumental in making sense of the photoelectric experiment.
Energy of Photon
\(E_{photon}\) energy of a photon.
\(\nu\) frequency of a single photon.
Thus we see that both matter and radiation is quantized and given by the same relation of frequency times Planck constant.
Kinetic energy: frequency vs intensity#
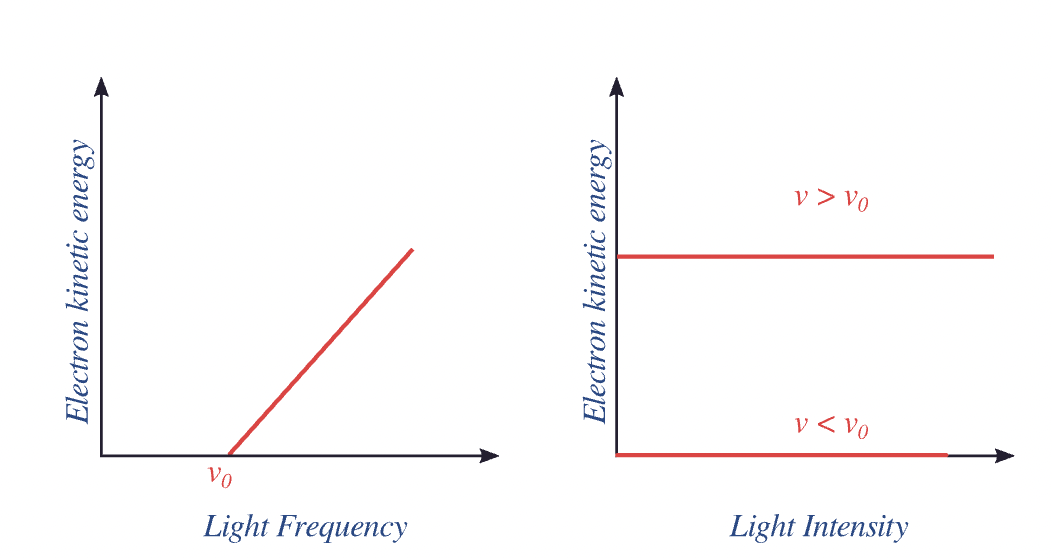
Fig. 17 Shown are dependece of electron kinetic energy on frequency of radiation that hits the surface of material (left plot) and on intensity of light for frequencies below and above threoshold (right plot).#
Frequency \(\nu\) determines weather electrons will be ejected: \(\nu>\nu_0\) but does not affect the number of electrons (current)
Kinetic energy of an ejected electron is a linearly increasing function of the frequency of light with no dependence on the intensity: \(KE\sim \nu\)
Contrary to wave theory of light increasing intensity (brighter) of light does not eject electrons when frequency is below the threshold \(\nu < \nu_0\)
Electric current: frequency vs intensity#
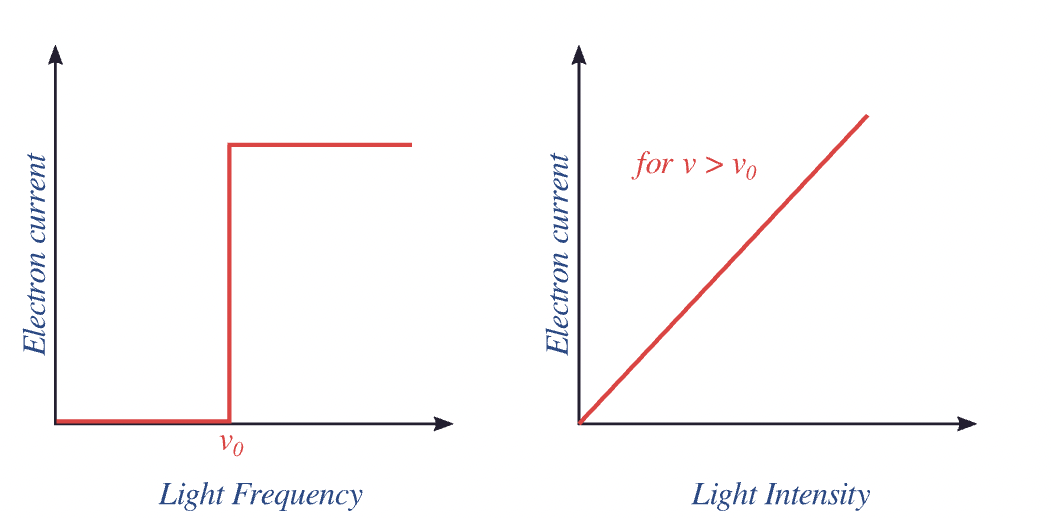
Fig. 18 Shown are dependece of electron current on frequency of radiation that hits the surface of material (left plot) and on intensity of light for some frequency above threoshold (right plot).#
Once threoshold is reached \(\nu>\nu_0\) frequency has no effect on electron current (number of electrons)
Once threoshold is reached \(\nu>\nu_0\) Increasing intensity of light on the other hand increases the current linearly.
Photons explain photoelectric effect#
Light consists of photons: tiny packets of energy carrying \(E_{photon}=h\nu\) energy.
Intensity of light quantifies number of photons.
Frequency of light quantifies energy of photons.
If light radiates \(n\) number of photons per second, then the total energy radiated per second is \(nh\nu\)
Particular nature of light 1 photon can “collide” with 1 electron and eject it if photon has sufficient energy.
Energy of photon = work function + kinetic energy of electron
The work function \(W_0=h\nu_0\) is the minimum amount of energy needed to remove an electron from a metal’s surface which has different values for different materials.
The \(\nu_0\) is threshold frequency: minimum frequecny needed to eject electron. If frequency is lower than threshold photon does not transfer any energy to the electron!
Any extra energy gets converted into kinetic energy \(KE=mv_e^2/2\) of the ejected electron, where \(v_e\) is the mangniture of ejected electron velcotiy.
Applications of photoelectric effect#

Fig. 19 Besides its historical role in the establishment of QM photoelectric effect has many practical applications. It is relevant for the design of solar cells, photovoltaics, photoelectron spectroscopy, night vision, etc. !#
Explore photoelectric effect#
Problems#
Problem 1#
Calculating the Threshold Frequency
A certain metal has a work function of 4.5 eV. Calculate the threshold frequency (\(\nu_0\)) required to emit electrons from the metal surface.
Solution:
The threshold frequency \(\nu_0\) is related to the work function \(\phi\) by the equation:
Where:
\(\phi = 4.5 \, \text{eV}\)
\(h = 4.1357 \times 10^{-15} \, \text{eV} \cdot \text{s}\) (Planck’s constant)
Now, solve for \(\nu_0\):
Problem 2#
Maximum Kinetic Energy of Photoelectrons
Ultraviolet light with a wavelength of 250 nm is incident on a metal surface with a work function of 3.0 eV. Calculate the maximum kinetic energy of the emitted photoelectrons.
Solution:
First, calculate the energy of the incident photons:
Where:
\(h = 6.626 \times 10^{-34} \, \text{J} \cdot \text{s}\)
\(c = 3.00 \times 10^8 \, \text{m/s}\)
\(\lambda = 250 \, \text{nm} = 250 \times 10^{-9} \, \text{m}\)
Convert this energy to eV:
The maximum kinetic energy \(K_{\text{max}}\) of the emitted photoelectrons is given by:
Problem 3#
Photoelectric Current and Light Intensity
Explain how the intensity of incident light affects the photoelectric current, assuming the frequency of the light is above the threshold frequency.
Solution:
In the photoelectric effect, the intensity of the incident light is proportional to the number of photons striking the metal surface per unit time. If the frequency of the light is above the threshold frequency, each photon has sufficient energy to eject an electron.
As the intensity increases, more photons hit the surface, leading to the emission of more photoelectrons. Consequently, the photoelectric current, which is proportional to the number of emitted electrons, increases with the intensity of the incident light. However, the kinetic energy of the emitted electrons remains the same and is determined by the energy of the individual photons, not the intensity of the light. , \text{eV} $$
