DEMO: Pertrubation Theory#
1. Energy Levels#
The unperturbed energy levels are given by:
\[ E_n^{(0)} = \frac{n^2 \pi^2 \hbar^2}{2 m L^2}, \quad n = 1, 2, 3, \dots \]The first-order correction to the energy is computed as:
\[ E_n^{(1)} = \langle \psi_n^{(0)} | V | \psi_n^{(0)} \rangle = \int_0^L \psi_n^{(0)}(x) V(x) \psi_n^{(0)}(x) \, dx \]The second-order correction to the energy accounts for interactions with other states:
\[ E_n^{(2)} = \sum_{m \neq n} \frac{|\langle \psi_m^{(0)} | V | \psi_n^{(0)} \rangle|^2}{E_n^{(0)} - E_m^{(0)}} \]In the left panel, the energy levels are plotted for:
\( E_n^{(0)} \): Unperturbed energy (blue line).
\( E_n^{(0)} + E_n^{(1)} \): First-order corrected energy (orange line).
\( E_n^{(0)} + E_n^{(1)} + E_n^{(2)} \): Second-order corrected energy (green line).
2. Wavefunctions#
The unperturbed wavefunction for state \( n \) is:
\[ \psi_n^{(0)}(x) = \sqrt{\frac{2}{L}} \sin\left(\frac{n \pi x}{L}\right) \]The first-order correction adds contributions from other states:
\[ \psi_n^{(1)}(x) = \sum_{m \neq n} \frac{\langle \psi_m^{(0)} | V | \psi_n^{(0)} \rangle}{E_n^{(0)} - E_m^{(0)}} \psi_m^{(0)}(x) \]The second-order correction further refines the wavefunction by including higher-order terms:
\[ \psi_n^{(2)}(x) = \sum_{m \neq n} \sum_{k \neq m} \frac{\langle \psi_k^{(0)} | V | \psi_m^{(0)} \rangle \langle \psi_m^{(0)} | V | \psi_n^{(0)} \rangle}{(E_n^{(0)} - E_m^{(0)})(E_m^{(0)} - E_k^{(0)})} \psi_k^{(0)}(x) \]In the right panel, the wavefunctions are plotted for:
\( \psi_n^{(0)}(x) \): Unperturbed wavefunction (blue line).
\( \psi_n^{(0)}(x) + \psi_n^{(1)}(x) \): First-order corrected wavefunction (orange line).
\( \psi_n^{(0)}(x) + \psi_n^{(1)}(x) + \psi_n^{(2)}(x) \): Second-order corrected wavefunction (green line).
Interactive Features#
Magnitude of the Perturbation (\( a \)):
Increasing \( a \) increases the influence of the perturbing potential, making corrections to the energy levels and wavefunctions more pronounced.
Quantum Number (\( n \)):
Higher \( n \) states exhibit larger deviations due to their higher energy levels and larger overlaps with the perturbing potential.
Define the problem#
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
from ipywidgets import interact
# Constants
L = 1 # Length of the box
hbar = 1 # Reduced Planck's constant
m = 1 # Mass of the particle
max_states = 10 # Number of states to include in corrections
# Unperturbed energy levels
def E_n_0(n):
return (n**2 * np.pi**2 * hbar**2) / (2 * m * L**2)
# Unperturbed wavefunction
def psi_n(x, n):
return np.sqrt(2 / L) * np.sin(n * np.pi * x / L)
# Perturbing potential: Quadratic potential
def V(x, a):
return a * x**2
# Matrix element <psi_m | V | psi_n>
def V_mn(m, n, a):
def integrand(x):
return psi_n(x, m) * V(x, a) * psi_n(x, n)
result, _ = quad(integrand, 0, L)
return result
First-order correction#
# First-order correction to energy
def first_order_correction(n, a):
return V_mn(n, n, a)
def psi_1_correction(x, n, a):
correction = np.zeros_like(x)
E_n0 = E_n_0(n)
for m in range(1, max_states + 1): # Sum over excited states
if m == n:
continue
E_m0 = E_n_0(m)
coeff = V_mn(m, n, a) / (E_n0 - E_m0)
correction += coeff * psi_n(x, m)
return correction
Second-order correction#
def second_order_correction(n, a):
correction = 0
E_n0 = E_n_0(n)
for m in range(1, max_states + 1):
if m == n:
continue
V_mn_value = V_mn(m, n, a)
correction += (abs(V_mn_value)**2) / (E_n0 - E_n_0(m))
return correction
def psi_2_correction(x, n, a):
correction = np.zeros_like(x)
E_n0 = E_n_0(n)
for m in range(1, max_states + 1): # Loop over intermediate states
if m == n:
continue
E_m0 = E_n_0(m)
coeff_mn = V_mn(m, n, a) / (E_n0 - E_m0)
for k in range(1, max_states + 1): # Loop over final states
if k == m:
continue
E_k0 = E_n_0(k)
coeff_mk = V_mn(k, m, a) / (E_m0 - E_k0)
correction += coeff_mn * coeff_mk * psi_n(x, k)
return correction
Visualizing corrections#
# Interactive plot function
def plot_energy_and_wavefunctions(a=1, n=1):
x = np.linspace(0, L, 1000) # Position grid
psi_0 = psi_n(x, n) # Unperturbed wavefunction
psi_1 = psi_1_correction(x, n, a) # First-order correction
psi_2 = psi_2_correction(x, n, a) # Second-order correction
psi_total = psi_0 + psi_1 + psi_2 # Total wavefunction
# Normalize corrected wavefunction
psi_total /= np.sqrt(np.trapz(psi_total**2, x))
# Energy levels
E0 = E_n_0(n)
E1 = first_order_correction(n, a)
E2 = second_order_correction(n, a)
# Plot
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
# Left panel: Energy levels
axes[0].hlines(E0, 0.5, 1.5, color='blue', label='Unperturbed $E_n^{(0)}$')
axes[0].hlines(E0 + E1, 1.5, 2.5, color='orange', label='1st Order $E_n^{(0)} + E_n^{(1)}$')
axes[0].hlines(E0 + E1 + E2, 2.5, 3.5, color='green', label='2nd Order $E_n^{(0)} + E_n^{(1)} + E_n^{(2)}$')
axes[0].set_title('Energy Levels')
axes[0].set_xticks([])
axes[0].set_ylabel('Energy')
axes[0].legend()
axes[0].grid(True)
# Right panel: Wavefunctions
axes[1].plot(x, psi_0, label='Unperturbed $\psi_n^{(0)}(x)$', color='blue')
axes[1].plot(x, psi_0 + psi_1, label='1st Order $\psi_n^{(0)}(x) + \psi_n^{(1)}(x)$', color='orange')
axes[1].plot(x, psi_total, label='2nd Order $\psi_n^{(0)}(x) + \psi_n^{(1)}(x) + \psi_n^{(2)}(x)$', color='green')
axes[1].set_title('Wavefunctions')
axes[1].set_xlabel('Position $x$')
axes[1].set_ylabel('Wavefunction $\psi(x)$')
axes[1].legend()
axes[1].grid(True)
plt.tight_layout()
plt.show()
# Create interactive sliders
interact(plot_energy_and_wavefunctions, a=(0, 25, 1), n=(1, 5, 1))
<function __main__.plot_energy_and_wavefunctions(a=1, n=1)>
Insights into Molecular Orbtials and Bonding from pertrubation theory perspective#
def molecular_orbital_energies(E_A, E_B, H_AB):
"""
Compute molecular orbital energies using perturbation theory.
"""
E_avg = (E_A + E_B) / 2
delta_E = (E_A - E_B) / 2
E_plus = E_avg + np.sqrt(delta_E**2 + H_AB**2) # Antibonding
E_minus = E_avg - np.sqrt(delta_E**2 + H_AB**2) # Bonding
return E_minus, E_plus
# Parameters
E_A_vals = np.linspace(-5, 0, 100) # Atomic orbital energy of A (e.g., 1s)
E_B = -4 # Fixed atomic orbital energy of B (e.g., 2s)
H_AB = 0.5 # Interaction strength
# Compute MO energies
bonding, antibonding = [], []
for E_A in E_A_vals:
E_minus, E_plus = molecular_orbital_energies(E_A, E_B, H_AB)
bonding.append(E_minus)
antibonding.append(E_plus)
# Plot results
plt.figure(figsize=(10, 6))
plt.plot(E_A_vals, bonding, label='Bonding MO ($E_-$)', color='blue')
plt.plot(E_A_vals, antibonding, label='Antibonding MO ($E_+$)', color='red')
plt.axhline(E_B, color='gray', linestyle='--', label='Atomic Orbital B')
plt.xlabel('Atomic Orbital Energy of A ($E_A$)')
plt.ylabel('Molecular Orbital Energy')
plt.title('Molecular Orbital Formation via Perturbation Theory')
plt.legend()
plt.grid(True)
plt.show()
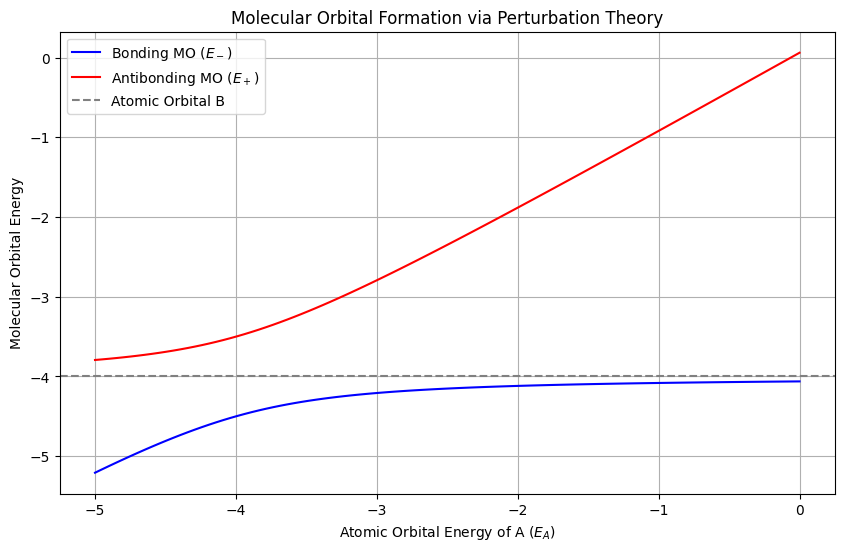
Roles of Bonding and Antibonding:
Bonding energy \( E_- \): Stabilized by \( -|H_{AB}|^2 / \Delta E \).
Antibonding energy \(E_+\): Destabilized by \( +|H_{AB}|^2 / \Delta E\).
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
def molecular_orbital_energies(E_A, E_B, H_AB):
"""
Compute molecular orbital energies using second-order perturbation theory.
"""
if E_A == E_B:
E_A += 1e-6 # Avoid division by zero
delta_E = E_A - E_B # Energy spacing
bonding = E_A - (H_AB**2 / delta_E) # Bonding MO
antibonding = E_B + (H_AB**2 / delta_E) # Antibonding MO
return bonding, antibonding
def plot_energy_levels(delta_E=2.0, H_AB=0.5):
"""
Visualize energy levels of atomic and molecular orbitals with second-order corrections.
"""
# Atomic orbital energies
E_B = -4.0 # Fixed AO energy of B
E_A = E_B + delta_E # Varying AO energy of A
# Molecular orbital energies
E_minus, E_plus = molecular_orbital_energies(E_A, E_B, H_AB)
# Plot energy levels
fig, ax = plt.subplots(figsize=(8, 6))
# Atomic orbital levels
ax.hlines(E_A, 0.2, 0.4, color='blue', label=f'Atomic Orbital A ($E_A = {E_A:.2f}$)')
ax.hlines(E_B, 0.2, 0.4, color='green', label=f'Atomic Orbital B ($E_B = {E_B:.2f}$)')
# Molecular orbital levels
ax.hlines(E_minus, 0.6, 0.8, color='orange', label=f'Bonding MO ($E_- = {E_minus:.2f}$)')
ax.hlines(E_plus, 0.6, 0.8, color='red', label=f'Antibonding MO ($E_+ = {E_plus:.2f}$)')
# Connect atomic and molecular orbitals
ax.plot([0.4, 0.6], [E_A, E_plus], color='gray', linestyle='--', linewidth=1)
ax.plot([0.4, 0.6], [E_B, E_minus], color='gray', linestyle='--', linewidth=1)
# Axis settings
ax.set_xlim(0.1, 0.9)
ax.set_ylim(-20, 20)
ax.set_ylabel('Energy')
ax.set_xticks([])
ax.set_title('Energy Levels with Second-Order Corrections')
ax.legend()
ax.grid(True)
plt.show()
# Create interactive sliders
interact(plot_energy_levels, delta_E=(-5.0, 5.0, 0.1), H_AB=5)
<function __main__.plot_energy_levels(delta_E=2.0, H_AB=0.5)>