Waves#
What you need to know
A wave is a self-propagating disturbance that transfers energy, momentum, and information through a medium, without transporting matter.
In quantum mechanics, waves are fundamental to understanding the behavior of particles at small scales.
The behavior of waves is governed by the wave equation, a partial differential equation (PDE) that describes their spatial and temporal evolution. This equation allows us to predict how a wave will propagate, oscillate, and interact with its environment.
Two major classes of waves we will be examining are Standing waves which remain fixed in space, exhibiting nodes and antinodes. Traveling waves which propagate through space, transferring energy from one location to another.
Additionally, waves can be classified as Transverse, where the disturbance is perpendicular to the direction of propagation, or Longitudinal, where the disturbance is parallel to the direction of propagation.
Types of Waves#
Disturbance of medium Sound Waves. Waves on a guitar string. Waves propogating on the surface of the water
Quantum mechanical waves They will be described by complex wavefunctions providing us expanation for the wave like behavior electrons and atoms.
Electromagnetic waves (e.g. light, UV, X-rays) this is the only kind of wave which does not require a medium! EM waves can travel in vacuum. In a sense, an EM wave “rolls out its own carpet” hence creating its own medium as it moves forward.
Gravitational waves traveling through spacetime!

Fig. 34 Visualiziing 1D propagating (or traveling) and standing waves waves. Traveling waves move with respect to a fixed reference frame. Standing waves move in place.#

Fig. 35 Transverse waves carry distrubance perpendicular to the direction of wave propogation. Longitudinal waves carry disturbance along the direction of wave propogation.#
Defining wave mathematically#
Since wave is a moving disturbance
Imagine surfing on an ocean wave. For an observer (surfer) standing on a wave the wave stands still at the same coordinate
For the observer standing on the shore the coordinate x of wave front moves away with a constant velocity:
Assuming that shape of the wave stays the same we can express the motion of wave in the reference frame of the still observer:
Periodic traveling waves.#
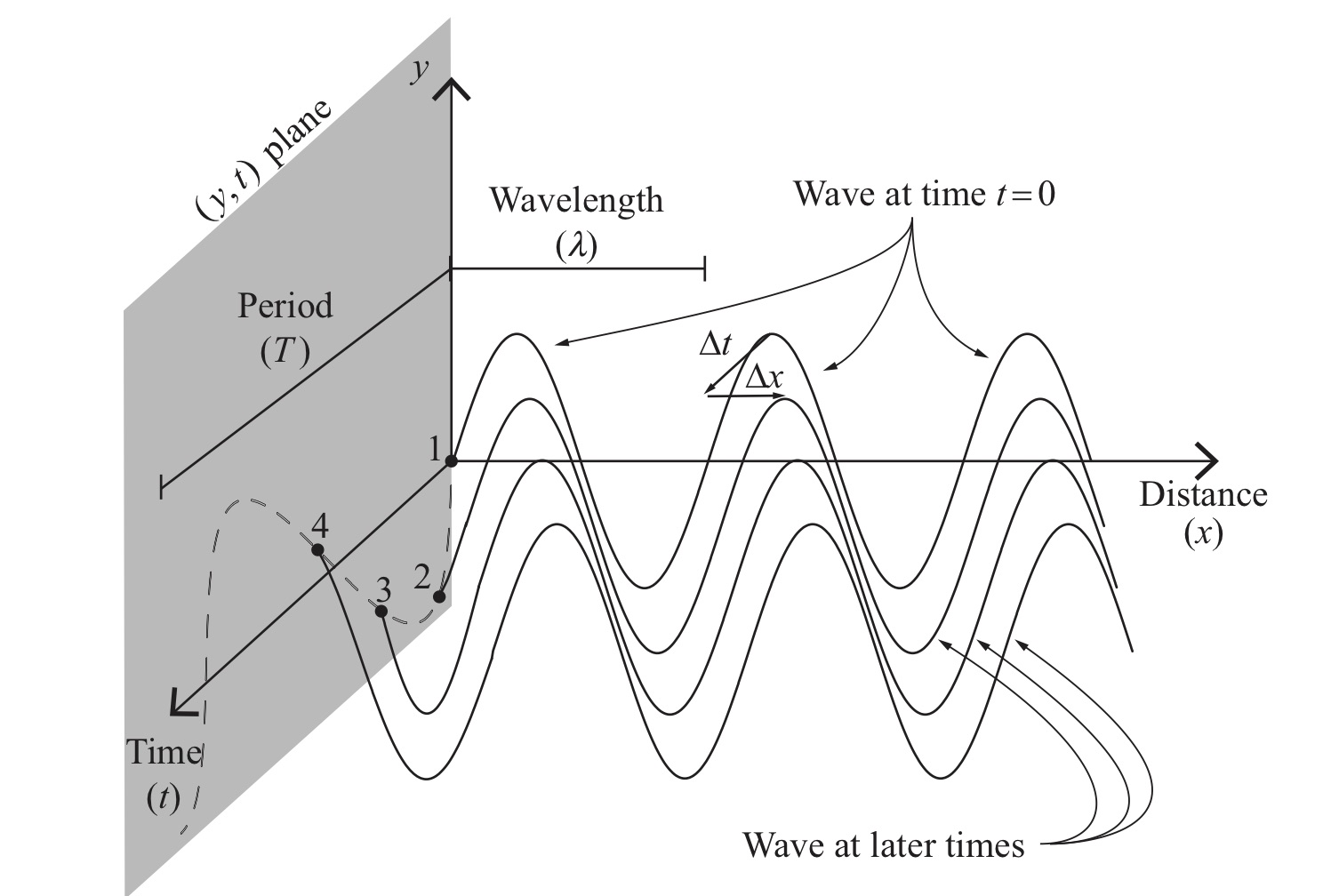
Fig. 36 Wave that is periodic in space and time#
We will be working a lot with periodic waves that have a periodic shape hence can be described by sine or cosine or their combination. Here is a general expression of sin wave:
Let us now turn this sinusoidal form into a wave traveling along x axis:
Amplitude
Wave number
Angular frequency
Initial phase
When describing waves it is much more convenient to work with complex representation. One can always extract real or imaginary part after calculations.
Complex exponential representation of waves
Periodicity in space and time#
Sine and cosine traveling waves are periodic in space and in time. We introduce two quantities that quantify these peridocities.
Periodic wave repeats itself at some values
Mathemtically this means every wavelength in space wave repeats its pattersn
Wavevectors
Periodic wave repeats itself at regular time periods
Mathemtically this means after every period wave repeats its pattersn
Angular frequency
The following expression makes it explicit that every multiple of
Wave equation.#
We obtain equation of motion by using the chain rule and taking partial derivatives of
Waves satisfy a wave equation
take two derivatives with respect to
take two derivatives with respect to
Now take the ration to replace u:
Just as in classical mechanics we need to take second derivative in order to get the equation of motion that is determined by initial position and velocity. By using the chain rule and taking one more derivative with respect to
Classical Wave Equation
We just obtained a 1D classical wave equation. Solutions of this equation are functions of time and space called wave functions.
Combinding waves: interference#
We are often interested in the result of multiple waves interacting with one another which can be described mathematically when we add up waves.
Combinging waves creates a new wave that again obyes wave equation. This known as the linear superposition principle if waves
Interference – a phenomenon of combining waves which results in a new wave of greater, lower, or the same amplitude.
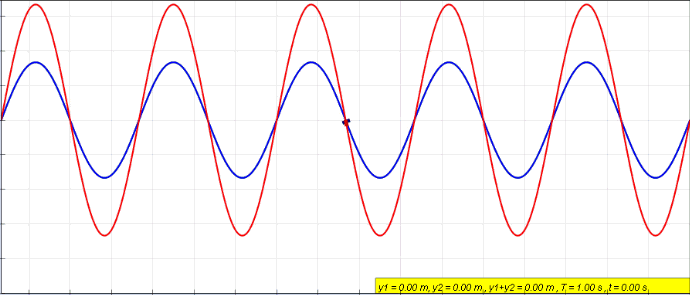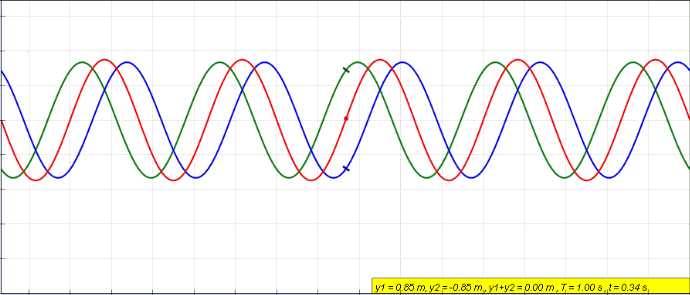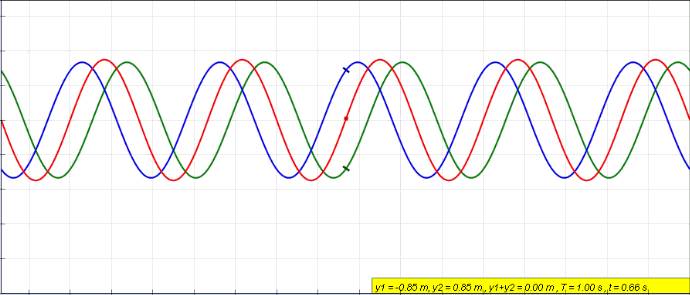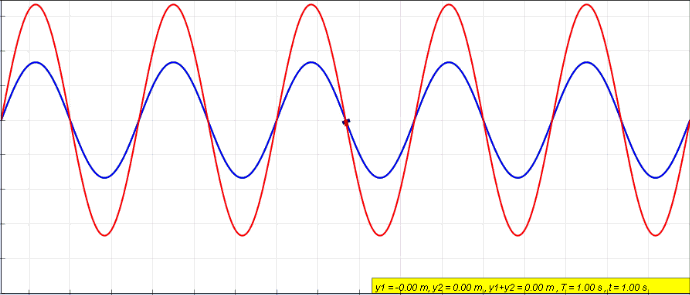
Fig. 37 Constructive vs destructive intereference of two cosine waves
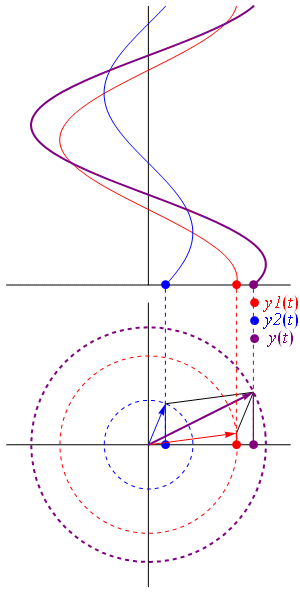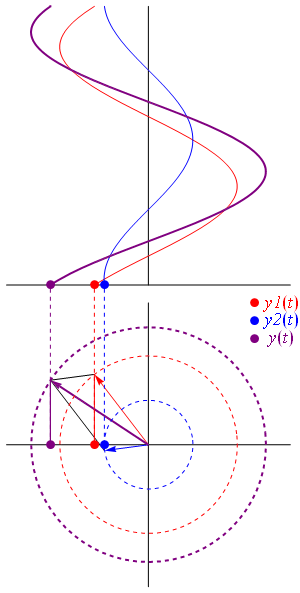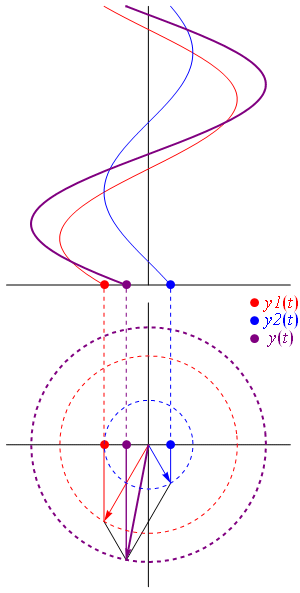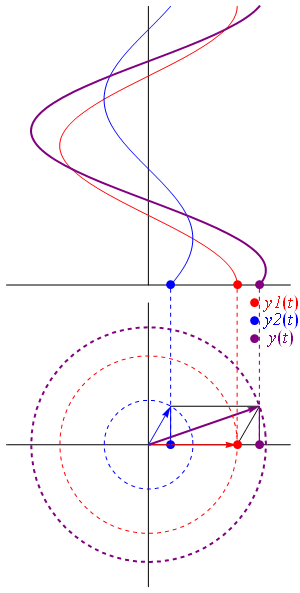
Fig. 38 Combining waves produces a new wave. Illlustrated using complex representation and real representation.#
Wave interference: derivation
Given the two waves:
We want to sum them:
Step-by-Step Derivation
Factor out the common exponential term
Use the exponential addition identity:
We can rewrite the sum of two exponentials with different phases
Simplify the remaining terms:
The term in parentheses is a sum of exponentials with opposite signs in the exponents, which is:
Substitute back:
Substitute this back into the expression for
Combine the exponents:
Finally, combine the exponents into one:
note that if phases differe by
Conclusion
Thus, the sum of two complex exponentials with different phases
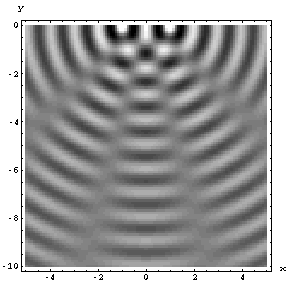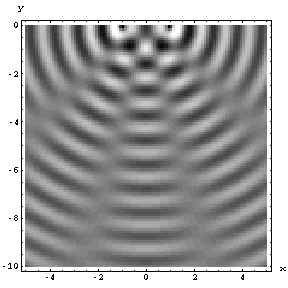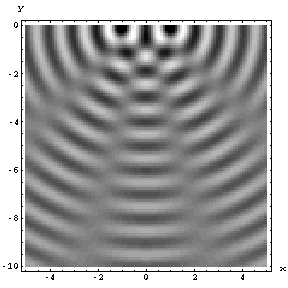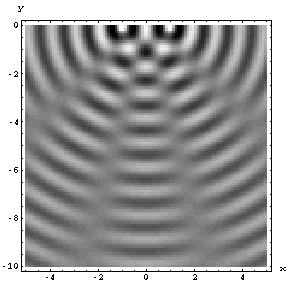
Fig. 39 Illustration of wave interference#
Example Problems#
Problem 1: Traveling or standing#
Which of the these functions can describe a traveling wave
Solution 1
If a function can be cast in the form
Problem 2: Wavelength and frequency#
Given a traveling sine wave
Solution 2
Traveling waves have
Now we can just read off some of the quantities
