Spin#
What You Need to Know
Magnetism arises from the circular motion of charged particles.
Atoms with electrons that have a non-zero orbital angular momentum generate magnetic moments, making them susceptible to the effects of an external magnetic field.
The Stern-Gerlach experiment established the existence of an intrinsic magnetic moment in electrons, called spin, which is affected by a magnetic field independently of orbital angular momentum.
Despite the name, spin is an intrinsic magnetic property of subatomic particles and does not involve literal “spinning” or motion. Spin is a fundamental property of particles, akin to mass or charge.
Particles with half-integer spins (e.g., \(1/2\), \(3/2\), \(5/2\)) are classified as fermions, while those with integer spins (e.g., 0, 1, 2) are classified as bosons. These two families of particles follow different rules. Fermions obey the Pauli exclusion principle, which states that no two identical fermions can occupy the same quantum state simultaneously (e.g., same position, velocity, and spin direction). In contrast, bosons are not restricted in this way and can occupy the same state, allowing them to “bunch together.”
Normal Zeeman Effect: This is the splitting of singlet states (spin zero) in a magnetic field due to the electron’s angular momentum, which can be explained classically.
Anomalous Zeeman Effect: This is a more general case where both electron spin and angular momentum contribute to the splitting of energy levels in a magnetic field.
Rotating charge generates mangetic moment#
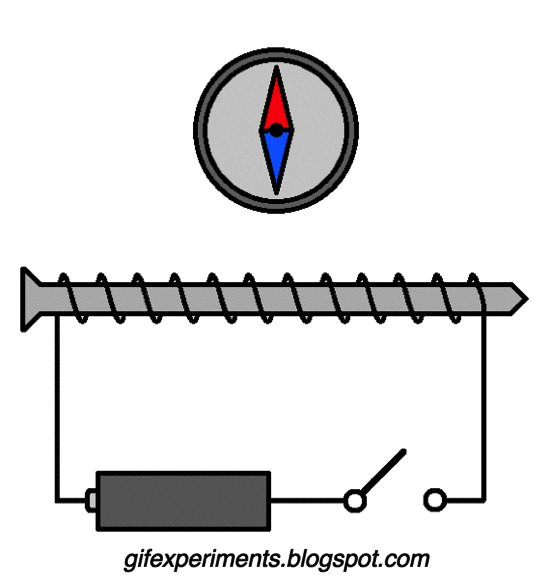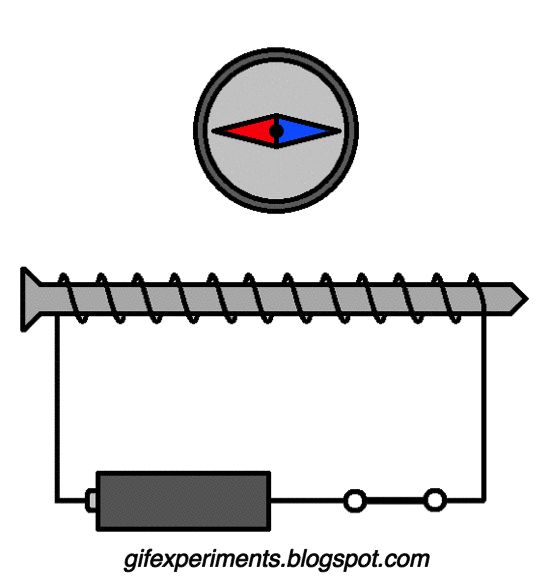
Fig. 80 A GIF demonstrating the existence of a magnetic field around a current carrying wire.#
A moving charge generates magnetic moment which interacts with an external magnetic field.
When an electron is in a state with \(l > 0\), one can think of a circular motion of charge (of the wavefunction describing electron) around the nucleus and generate its own magnetic field.
Note that this motion is not classical but here we are just trying to obtain a wire frame model based on classical interpretation.
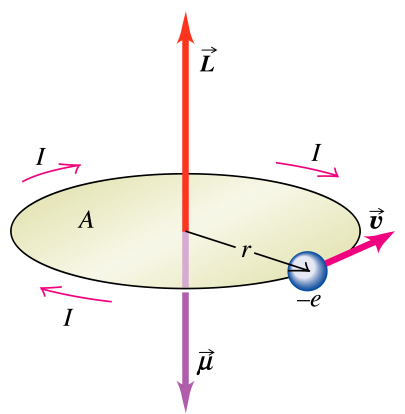
Fig. 81 Shown are magnetic moment and angular momentum generated by a charge moving on an obrit.#
Magnetic moment of electron#
According to classical mechanics a charged particle like an electron that is rotating around an axis has a magnetic moment given by:
where \(\gamma_e\) is the magnetogyric ratio of the electron expressed via fundamental constants (\(-\frac{e}{2m_e}\)) We choose the external magnetic field to lie along the \(z\)-axis and therefore it is important to consider the \(z\) component of \(\vec{\mu}\):
where \(\mu_B\) is the Bohr magneton as defined above. The interaction between a magnetic moment and an external magnetic field is given by (classical expression):
Where \(\alpha\) is the angle between the two magnetic field vectors. This gives the energy for a bar magnet in presence of an external magnetic field:

Fig. 82 External magnetic field exerts torque on magnet. The energy of itneraction between the field and magnetic is proprotional to the strength of the field \(B\) and magnetic moment of the magnetic \(\mu\)#
Unlike quantum mechanics in classical mechanics any orientation is allowed. When the external magnetic field is oriented along \(z\)-axis the potential energy of interaction with field in classical mechanics is:
In quantum mechanics to get the hamilotnian term or interaction with magnetic field we simply need to replace classical angular momentum with corresponding operator
Effect of magnetic field on atoms#
In quantum mechanics, a magnetic moment (here corresponding to a non \(s\) orbital electron) may only take specific orientations!
The \(z\)-axis is often called the quantization axis. The eigenvalues of \(\hat{L}_z\) essentially give the possible orientations of the magnetic moment with respect to the external field.
For example, consider an electron on \(2p\) orbital in a hydrogenlike atom. The electron may reside on any of \(2p_{+1}\), \(2p_0\) or \(2p_{-1}\) orbitals (degenerate without the field). For these orbitals \(L_z\) may take the following values (\(+\hbar, 0, -\hbar\)):
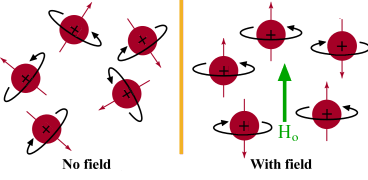
Fig. 83 External amgnetic field orients atoms with dipole moments due to electrons in non-zero l orbitals.#
Mangetic field modifies the Hamiltonian#
The relative orientations with respect to the external magnetic field are shown on the left side of the figure. The total quantum mechanical Hamiltonian for a hydrogenlike atom in a magnetic field can now be written as:
where \(\hat{H}_0\) denotes the Hamiltonian in absence of the magnetic field.
Since projection of angular momentum commutes with Hamitlonian \([\hat{L}_z, \hat{H}_0]=0\) we have same eigenfunctions for both:
H-atom in magneitic field
\(n = 1, 2, ...\); determines energy levels in absence of magnetic field \(E_n\)
\(\beta_B = \frac{\hbar e}{2 m_e}\) constant we call Bohr’s magneton.
\(m_l = -l, ..., 0, ..., +l\).
Zeeman effect#
We seee that quantum magnetic field now enters in the expression determining energy levels in presence o mag field.
Mag ield now splits \((2l + 1)\) degenerate levels. This is called the orbital Zeeman effect.
For instance the 2p level of hydrogen atom will split into 3 levels \(-\beta_B B, 0,+\beta_B\)
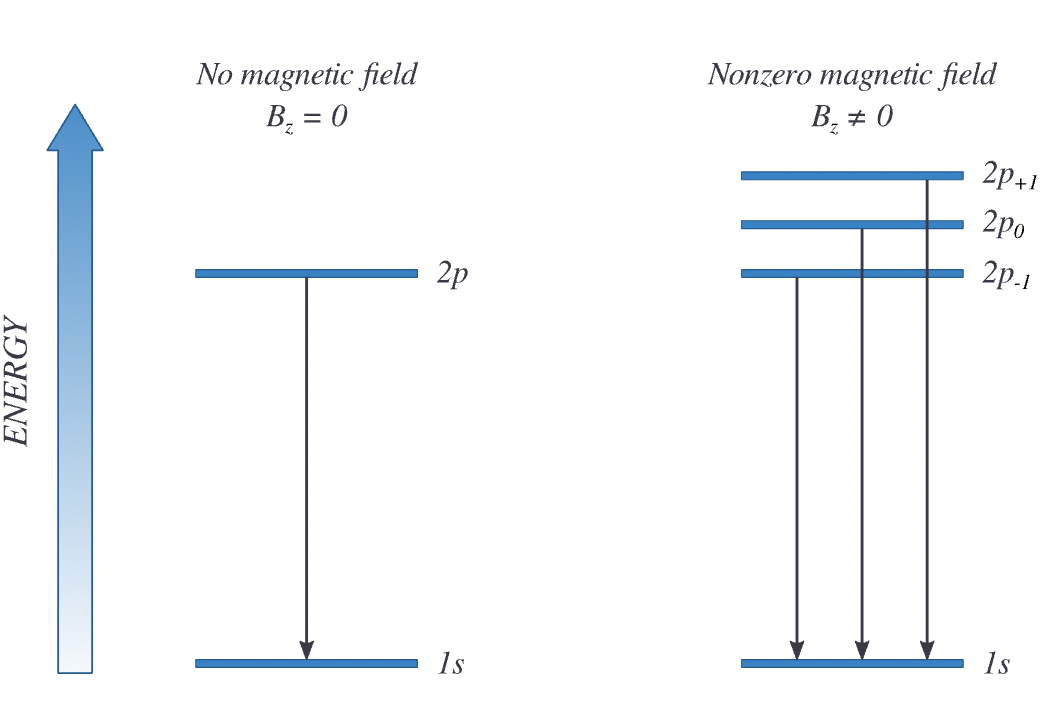
Fig. 84 Zeeman effect When an external magnetic field is applied, sharp spectral lines hydrogen split into multiple closely spaced lines. Shown are the splitting of the degenerate energy levels of 2p into three states differing in \(m_l=-1, 0, +1\)#
Disocvering Spin#
Spin as a tiny magnet#
We come to view spin of subatomic particles in a same way as we view mass and charge. Spin is an intrinsic property of subatomic particles like protons and electrons and photons.
Spin manifests itself via a permanent magnetic moment. A particle with spin can interact with magnetic fields just like particles with charge can interact with electric fields. This is why spin is pictorially depcited as tiny manget.
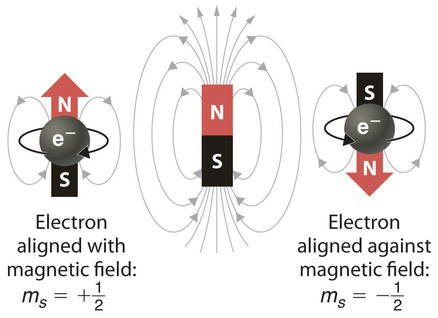
The Schrödinger equation does not naturally account for electron spin! This is because spin lacks a classical analogue, so our approach of taking the classical Hamiltonian and replacing terms with operators doesn’t work directly for spin.
The concept of electron spin originates from the Dirac equation, which is essentially a generalization of the Schrödinger equation to include relativistic effects.
Fortunately, spin can be incorporated into the Schrödinger equation once we recognize its existence. We simply add an additional quantum number, \(s\), which behaves similarly to angular momentum \(l\).
Quantum numbers and eigenfunctions of spins#
Spin and its projection, \(S\), \(S_z\) have the same properties as the angular momentum \(L\), \(L_z\). Quantum mechanics requires the number of allowed spin projections to be:
Experiments show that we only observe two values of spin.
Projections are determined by quantum number \(m_s\) which is an analog of \(m_l\)
We expect two eigenfunctons for two outcomes and denote the eigenfunctions of \(S_z\) as \( \alpha \) and \( \beta \):
Eigenfunctions of Spin \( \alpha \) and \( \beta \)
Spin is an intrinsic angular momentum with a fixed eigenvalue
Spin eigenfunctions and eigenvalues
Orthogonality and normalization of spin part of wavefunction#
Note that the following operators commute: \( \hat{H} \), \( \hat{L}^2 \), \( \hat{L}_z \), \( \hat{S}^2 \), and \( \hat{S}_z \). This implies that all these quantities can be specified simultaneously.
The spin eigenfunctions \( \alpha \) and \( \beta \) are as expected orthonormal:
To completely describe a hydrogen-like atom, the wavefunction must include the spin component. Thus, the total wavefunction is a product of the spatial wavefunction and the spin part.
Wavefuncctions differing in spin part will be orthogonal!
Action of Spin Operators on Eigenstates
In quantum mechanics, the spin of an electron is represented by the spin operator \( \vec{S} \), which has components \( S_x \), \( S_y \), and \( S_z \). For spin-\(\frac{1}{2}\) particles, these operators are represented by the Pauli matrices \( S_x \), \( \sigma_y \), and \( \sigma_z \) (multiplied by \(\frac{\hbar}{2}\)):
The Pauli matrices are:
The spin eigenstates \( \alpha \) and \( \beta \) correspond to the “spin-up” and “spin-down” states along the \( z \)-axis and are represented as:
\( S_z \) Operator:
Applying \( S_z \) to \( \alpha \) and \( \beta \):
\[\begin{split} S_z \alpha = \frac{\hbar}{2} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \frac{\hbar}{2} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \frac{\hbar}{2} \alpha \end{split}\]\[\begin{split} S_z \beta = \frac{\hbar}{2} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = -\frac{\hbar}{2} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = -\frac{\hbar}{2} \beta \end{split}\]Thus, \( S_z \) acts on \( \alpha \) and \( \beta \) as follows:
\( S_z \alpha = \frac{\hbar}{2} \alpha \)
\( S_z \beta = -\frac{\hbar}{2} \beta \)
\( S_x \) Operator:
Applying \( S_x \) to \( \alpha \) and \( \beta \):
\[\begin{split} S_x \alpha = \frac{\hbar}{2} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \frac{\hbar}{2} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \frac{\hbar}{2} \beta \end{split}\]\[\begin{split} S_x \beta = \frac{\hbar}{2} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \frac{\hbar}{2} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \frac{\hbar}{2} \alpha \end{split}\]So, \( S_x \) acts on \( \alpha \) and \( \beta \) as:
\( S_x \alpha = \frac{\hbar}{2} \beta \)
\( S_x \beta = \frac{\hbar}{2} \alpha \)
\( S_y \) Operator:
Applying \( S_y \) to \( \alpha \) and \( \beta \):
\[\begin{split} S_y \alpha = \frac{\hbar}{2} \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \frac{\hbar}{2} \begin{pmatrix} 0 \\ i \end{pmatrix} = \frac{i \hbar}{2} \beta \end{split}\]\[\begin{split} S_y \beta = \frac{\hbar}{2} \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \frac{\hbar}{2} \begin{pmatrix} -i \\ 0 \end{pmatrix} = -\frac{i \hbar}{2} \alpha \end{split}\]Thus, \( S_y \) acts on \( \alpha \) and \( \beta \) as follows:
\( S_y \alpha = \frac{i \hbar}{2} \beta \)
\( S_y \beta = -\frac{i \hbar}{2} \alpha \)
Summary Table
Operator |
\( \alpha \) (Spin-Up) |
\( \beta \) (Spin-Down) |
|---|---|---|
\( S_z \) |
\( \frac{\hbar}{2} \alpha \) |
\( -\frac{\hbar}{2} \beta \) |
\( S_x \) |
\( \frac{\hbar}{2} \beta \) |
\( \frac{\hbar}{2} \alpha \) |
\( S_y \) |
\( \frac{i \hbar}{2} \beta \) |
\( -\frac{i \hbar}{2} \alpha \) |
Mangetic moment due to spin#
Note that analogously, the \(\hat{S}_x\) and \(\hat{S}_y\) operators can be defined. These do not commute with \(\hat{S}_z\). Because electrons have spin angular momentum, the unpaired electrons in silver atoms (Stern-Gerlach experiment) produce an overall magnetic moment (``the two two spots of silver atoms’’). The spin magnetic moment is proportional to its spin angular momentum:
where \(g_e\) is the free electron \(g\)-factor (2.002322 from quantum electrodynamics). The \(z\)-component of the spin magnetic moment is (\(z\) is the quantiziation axis):
Hamiltonian depends on spin operator#
Following the eigenfunctions of \(S_z\) obtained above the corresponding eigenvalues for spin mangetic moment will be:
Thus the total energy for a spin in an external magnetic field is:
where \(B\) is the magnetic field strength (in Tesla). By combining the contributions from the hydrogenlike atom Hamiltonian and the orbital and electron Zeeman terms, we have the total Hamiltonian:
The eigenvalues of this operator are (derivation not shown):
Spin-Orbit coupling#
Having two source of mangeitc fields in atoms one due to orbtial momentum and another due to spin there arises a possibility that these microscopic magnets can interact.
And such a possibility is indeed realized and known as spin-orbit coupling! A new term is added to hamitlonian to account for this fact.
Where the A is a constant, \(\hat{H}_0\) hamiltonain for H-atom without spin and \(\hat{L}\) and \(\hat{S}\) are operators for total angular and spin momentum. Notice two things here: one, the term decays as \(1/r^3\) that is faster than potential energy hence this term makes much smaller contribution compared to hamiltonian for H-atom \(\hat{H}_0\).
Secondly becasue of spin-orbit coupling neither \(\hat{L}\) nor \(\hat{S}\) commute with hamiltonian! Hence one needs a new quantum number \(J\) to specify H-atom states. - This new quantum number is total angular momentum \(J+L+S\)
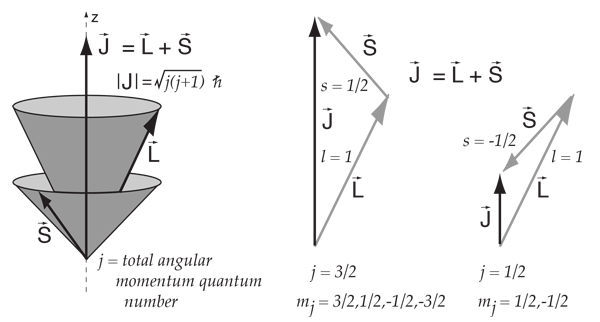
Fig. 85 Determining the values of total angular momentum \(j=l+s\) by using the fact that projections \(m_j\) are given as scalar sum of projections of angular and spin quantum numbers \(m_j=m_l+m_s\) and that \(j\) values follow the anuglar momentum quantization and assume \(2j+1\) values. Shown is the example of determining microstates for \(l=1\) state of H-atom (\(2p^1\)) orbital which gives rise to \(^2P_{3/2}\) and \(^2P_{1/2}\) microstates.#
Determine total angular momentum values for H atom#
Understand Angular Momentum Coupling: In a hydrogen atom, the total angular momentum \( \vec{J} \) is the vector sum of the orbital angular momentum \( \vec{L} \) and the spin angular momentum \( \vec{S} \):
\[ \vec{J} = \vec{L} + \vec{S} \]Here:
\( l \) is the orbital angular momentum quantum number, which takes integer values \( l = 0, 1, 2, \dots \)
\( s \) is the spin quantum number. For an electron, \( s = \frac{1}{2} \).
Determine Possible \( j \) Values:
The quantum number \( j \) represents the magnitude of the total angular momentum \( \vec{J} \). The possible values of \( j \) are given by the range:
\[ j = |l - s|, |l - s| + 1, \dots, (l + s) \]This range includes all integer or half-integer steps from \( |l - s| \) up to \( l + s \).
Calculate \( j \) Values Based on \( l \) and \( s \):
Since \( s = \frac{1}{2} \) for a single electron, the possible values of \( j \) will depend on the specific value of \( l \) as follows:
If \( l = 0 \):
\[ j = |0 - \frac{1}{2}| = \frac{1}{2} \]So, the only possible value for \( j \) is \( j = \frac{1}{2} \).
If \( l = 1 \):
\[ j = |1 - \frac{1}{2}| = \frac{1}{2} \quad \text{and} \quad j = 1 + \frac{1}{2} = \frac{3}{2} \]Thus, the possible values for \( j \) are \( j = \frac{1}{2} \) and \( j = \frac{3}{2} \).
If \( l = 2 \):
\[ j = |2 - \frac{1}{2}| = \frac{3}{2} \quad \text{and} \quad j = 2 + \frac{1}{2} = \frac{5}{2} \]The possible values for \( j \) are \( j = \frac{3}{2} \) and \( j = \frac{5}{2} \).
In General:
For any integer \( l \), the possible values of \( j \) will be \( l \pm \frac{1}{2} \).
Interpretation of \( j \) Values: These \( j \) values correspond to the quantized total angular momentum for the hydrogen atom. The total angular momentum \( J \) has a magnitude of \( \sqrt{j(j+1)} \hbar \). The \( j \) values determine the energy level splitting in the presence of fine structure interactions, where the spin-orbit coupling affects the energy depending on \( j \).
To Summarize Given an orbital angular momentum quantum number \( l \) and electron spin \( s = \frac{1}{2} \), the possible values of \( j \) are \( j = l \pm \frac{1}{2} \). This derivation is crucial in understanding fine structure in hydrogen atoms and the splitting of spectral lines due to spin-orbit coupling.
Term Symbols#
Becsue of spint orbit coupling the energy levels are no longer diescribed by \(l\) and \(s\) separetely. This is why one introduces term sybols to describe new states with total spin multiplicity \((2S+1)\) and anuglar momentum \(L\) and total angular momentum \(J=L+S\). The word total will take more meaning when we discuss multi electorn atoms where angular moenta are summed. For H-atom \(S=1/2\) and \(L=l\)

Fig. 86 Allowed values of the total angular momentum \(j\)#
Example:
Determine the microstates of l=1 and l=2 resulting from spin-orbit coupling.
Solution
The \(j=l+s\) values follow the rules of spatial quantization of angular momentum just like \(l\) and \(s\). That is the projection of \(J\), the \(m_j\) can only take \(l+s, l+s-1,...l-s\) values. Since \(s=1/2\) we are left with \(l+1/2\) and \(l-1/2\) values of \(m_j\). Note that the total number of microstates is equal to 2 values of \(m_s\) \(+1/2, -1/2\) and \(2l+1\) values of \(m_l\). In total we expect \(2(2l+1)\) microstates.
For \(l=1\) we identify \(m_j=1+1/2=3/2\) the maximum projection which is coming from j=3/2 valyes. We also idenitfy \(m_j=l-1/2=1/2\) the minimum projection which should come from \(j=1/2\). We thus have two microstates!
“Anomalous” Zeeman Effect#
While the Zeeman effect in some atoms (e.g., hydrogen) showed the expected equally-spaced triplet, in other atoms the magnetic field split the lines into four, six, or even more lines and some triplets showed wider spacings than expected. These deviations were labeled the anomalous Zeeman effect and were very puzzling to early researchers.
The explanation of these different patterns of splitting gave additional insight into the effects of electron spin. With the inclusion of electron spin in the total angular momentum, the other types of multiplets formed part of a consistent picture. So what has been historically called the “anomalous” Zeeman effect is really the normal Zeeman effect when electron spin is included.
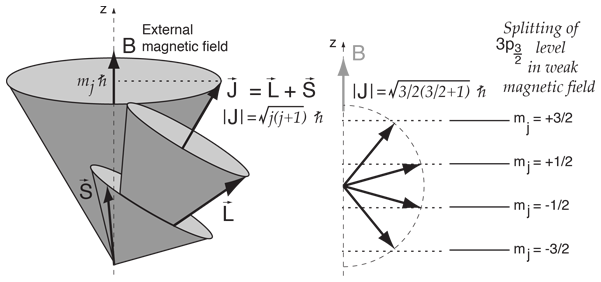
Fig. 87 In the presence of magnetic field the spectral lines are split further into levels described by \(m_J\).#
When magnetic field is applied to \(H\) atom the external field \(B\) now interacts with the total combined angular momentum \(J\) which results in splitting of energy values of each level with distinct \(J\). That is \(^2P_{3/2}\) is split into \(2\cdot 3/2+1=4\) lines and \(^2P_{1/2}\) is split into \(2\cdot 1/2+1=2\) lines.
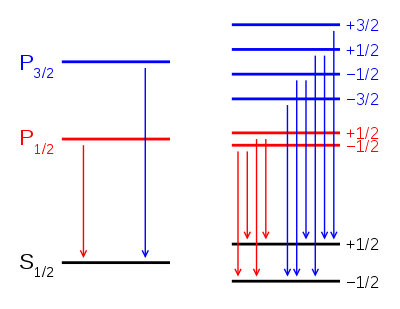
Fig. 88 Anomalous Zeeman effect. (left) The spectral lines are split into multiple microstates becasue of spin-orbit coupling. Energy states are described by term symbols (right) With weak magnetic field the lines are split further acording to values of \(j\) and its projection \(m_j\).#
Selection rules for electronic transitions#
Just like with energetic transitions of other model systems for H-atom probability of transition is given by transition moment or its z-projection \(\langle n,l,m_l, m_s |z|n,l,m_l, m_s \rangle\). Evaluating the expression using properties of special functions we get the following selection rules
Selection rules for electronic transitions in H atom
Summary of spin and angular momentum#
Spin emerges naturally once one accounts for relativistic effect, as was originally shown by Paul Dirac. Except for special cases relativisti effects however are not too significant to include in quantum mechanics therefore we incoprorate spin as an additional degree of freedom which has not been accounted for but which is knwon to exist!
Angular momentum |
Spin momentum |
|---|---|
\(\hat{L}=\hat{r}\times \hat{p}\) |
\(\hat{S}\) |
\(l=0,1,2,3,...\) |
\(s=1/2\) |
\(\mid l,m_l\rangle=Y_{l, m_l}\) |
\(\mid s,m_s\rangle=\alpha,\beta\) |
\(L=\hbar\sqrt{l(l+1)}\) |
\(S=\hbar\sqrt{s(s+1)}=\hbar\sqrt{3/4}\) |
\(\mu_L=- g_l \frac{e}{2m_e}L\) |
\(\mu_S = g_s \frac{e}{2m_e}S\) |
Problems#
Problem-1#
Why is it sufficient to specify \(|s, m_s\rangle\) for spin states
Hint
Use the analogy with angular momentum
Problem-2#
Why we use four quantum numbers \(n\), \(l\), \(m_l\), \(m_s\) to specify H-atom states \(|1, 0, 0, +1/2\rangle\) for instance.
What can we say about operators whose eigenvalues are defined in terms of these quantum numbers?
Hint
These quantum numbers uniquely specify the state of H-atom. That is we can simultaneosuly measure all quantum numbers.
Think of commutation relation
Problem-3#
Determine microstates of H-atom correpsonding to \(l=4\)