Multi-electron atoms

What you need to know

• We approximate many-electron wavefunctions using hydrogenic orbitals as building blocks.

• Unlike the hydrogen atom, multi-electron problems do not separate and therefore do not admit exact analytical solutions.

• Spin and antisymmetry impose strict constraints on allowed electronic wavefunctions.

Orbital Approximation

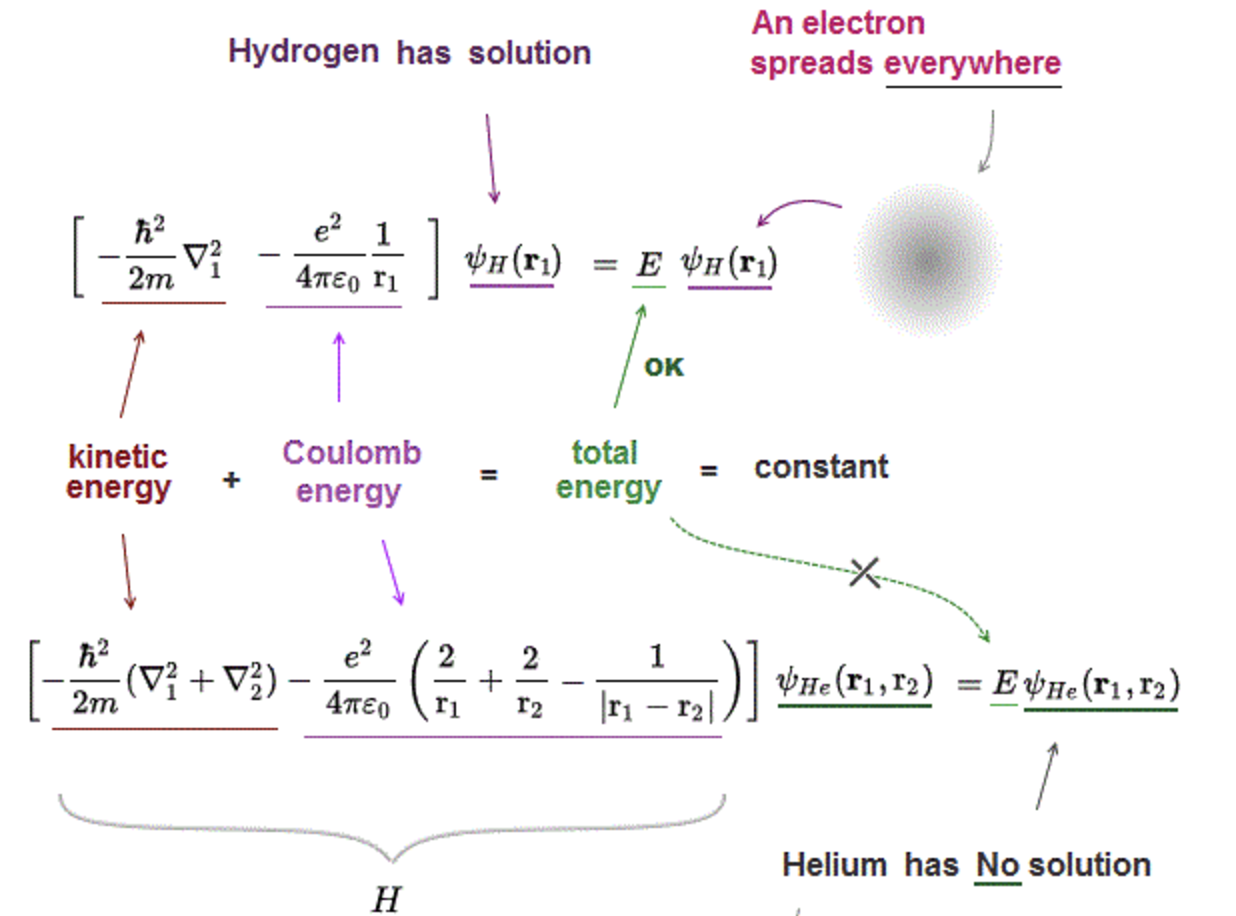
Fig. 90 Difference between the hydrogen and helium Hamiltonians that makes multi-electron atoms analytically unsolvable.

• For multi-electron atoms, the Hamiltonian depends on the coordinates of all electrons. The coordinates cannot be separated, so the Schrödinger equation is not analytically solvable.

• A practical approximation is to represent the wavefunction as a product of single-electron orbitals:

  • These orbitals are obtained computationally (e.g., variationally).

Orbital Approximation

\[ \Psi(r_1, r_2, \ldots, r_n) \approx \phi_1(r_1)\phi_2(r_2)\cdots\phi_n(r_n) \]

• \(\Psi\) is the multi-electron wavefunction.

• Each \(\phi_i(r)\) is an atomic orbital occupied by one electron.

Helium Wavefunction

For helium, the simplest guess would be

\[ \Psi(r_1, r_2) \approx \phi_1(r_1)\phi_2(r_2). \]

This form, however, suffers from three fundamental issues:

1. Indistinguishability Electrons are identical; the wavefunction cannot assign “electron 1” to “orbital 1” and “electron 2” to “orbital 2.”

2. Missing spin information The spatial wavefunction must combine with a spin function so that the total wavefunction is antisymmetric.

3. Neglect of electron–electron correlation The product form assumes electrons move independently, which leads to quantitative errors in energies.

Issue 1: Indistinguishability and Antisymmetry

Particles such as electrons are indistinguishable. Therefore the probability density must remain unchanged upon interchange:

\[ |\Psi(r_1,r_2)|^2 = |\Psi(r_2,r_1)|^2, \]

which implies

\[ \Psi(r_1,r_2) = \pm \Psi(r_2,r_1). \]

Electrons are fermions, and Pauli’s principle dictates that their total wavefunction must be antisymmetric:

Antisymmetry Requirement

\[ \Psi(\ldots, r_m, \ldots, r_n, \ldots) = -\Psi(\ldots, r_n, \ldots, r_m, \ldots). \]

A simple way to generate symmetric/antisymmetric forms for a two-variable function \(f(x,y)\):

• Symmetric:

  \[ g_+(x,y) = f(x,y) + f(y,x) \]

• Antisymmetric:

  \[ g_-(x,y) = f(x,y) - f(y,x) \]

For helium, the antisymmetrized spatial wavefunction is

\[ \Psi(r_1,r_2) \propto \phi_1(r_1)\phi_2(r_2) - \phi_1(r_2)\phi_2(r_1). \]

Issue 2: Spin Requirement

Electrons have two spin states, \(\alpha\) and \(\beta\). The total wavefunction (spatial × spin) must be antisymmetric:

• If spatial part is symmetric, spin part must be antisymmetric.

• If spatial part is antisymmetric, spin part must be symmetric.

• Symmetric spin part:

  \[ \alpha(1)\alpha(2) \]
  \[ \beta(1)\beta(2) \]
  \[ \frac{1}{\sqrt{2}}\left[\alpha(1)\beta(2) + \alpha(2)\beta(1)\right] \]

• Antisymmetric spin part:

  \[ \frac{1}{\sqrt{2}}\left[\alpha(1)\beta(2) - \alpha(2)\beta(1)\right] \]

Pauli Exclusion Principle

A key result of antisymmetry is the Pauli Exclusion Principle:

No two electrons can possess identical sets of quantum numbers.

For helium’s ground state (\(1s^2\)), the properly antisymmetrized total wavefunction is

\[ \Psi = \frac{1}{\sqrt{2}} \left[1s(1)1s(2) + 1s(2)1s(1)\right] \left[\alpha(1)\beta(2) - \alpha(2)\beta(1)\right]. \]

Slater Determinants

• Slater introduced a compact and universally applicable way to construct antisymmetric many-electron wavefunctions:

  • A determinant expands into an antisymmetric sum of products of one-electron spin-orbitals

  • Any exchange of two electrons flips the sign of the wavefunction

  • This guarantees the Pauli exclusion principle is satisfied automatically

Slater Determinant

\[\begin{split} \Psi(r_1,\ldots, r_n) = \frac{1}{\sqrt{n!}} \begin{vmatrix} \chi_1(1) & \chi_2(1) & \cdots & \chi_n(1) \\ \chi_1(2) & \chi_2(2) & \cdots & \chi_n(2) \\ \vdots & \vdots & \ddots & \vdots \\ \chi_1(n) & \chi_2(n) & \cdots & \chi_n(n) \end{vmatrix} \end{split}\]

• \(\chi_j(i)\) is a spin-orbital, i.e., orbital × spin function, describing electron i) in spin-orbital \(j\)

• The factor \(1/\sqrt{n!}\) ensures proper normalization of the determinant

• For example helium ground state Slater determinant looks like this

\[\begin{split} \Psi_{He} = \frac{1}{\sqrt{2}} \begin{vmatrix} 1s(1)\alpha(1) & 1s(1)\beta(1) \\ 1s(2)\alpha(2) & 1s(2)\beta(2) \end{vmatrix} \end{split}\]

• For Lithium ground state Slater determinant looks like this

\[\begin{split} \Psi_{\text{Li}} = \frac{1}{\sqrt{3!}} \begin{vmatrix} 1s(1)\alpha(1) & 1s(1)\beta(1) & 2s(1)\alpha(1) \\ 1s(2)\alpha(2) & 1s(2)\beta(2) & 2s(2)\alpha(2) \\ 1s(3)\alpha(3) & 1s(3)\beta(3) & 2s(3)\alpha(3) \end{vmatrix} \end{split}\]

Singlet and Triplet Excited States of Helium

When one electron occupies (1s) and the other (2s), their spatial wavefunctions can be combined as:

Spatial states

\[ \Psi_{\text{S}}(1,2) = \frac{1}{\sqrt{2}}\left[1s(1)2s(2) + 1s(2)2s(1)\right] \qquad\text{(symmetric)}, \]

\[ \Psi_{\text{A}}(1,2) = \frac{1}{\sqrt{2}}\left[1s(1)2s(2) - 1s(2)2s(1)\right] \qquad\text{(antisymmetric)}. \]

• Because electrons are fermions, the total wavefunction must be antisymmetric:

\[ \underbrace{\text{(spatial symmetry)}}_{\Psi_{S/A}} \times \underbrace{\text{(spin symmetry)}}_{\chi_{S/A}} = \text{antisymmetric} \]

• The total two-electron wavefunction must be antisymmetric:

\[ \Psi_{\text{total}}(1,2) = \Psi_{\text{spatial}}(1,2)\,\chi_{\text{spin}}(1,2). \]

Triplet states (\(S=1\) and symmetric spin)

• Must pair with the antisymmetric spatial part \(\Psi_A(1,2)\).

Spin functions:

\[\begin{split} \begin{aligned} \chi_{+1} &= \alpha(1)\alpha(2) \\ \chi_{0} &= \frac{1}{\sqrt{2}}\!\left[\alpha(1)\beta(2)+\beta(1)\alpha(2)\right] \\ \chi_{-1} &= \beta(1)\beta(2) \end{aligned} \end{split}\]

Total wavefunctions:

\[ |\psi_{+1}\rangle = \Psi_A(1,2)\,\chi_{+1} \]

\[ |\psi_{0}\rangle = \Psi_A(1,2)\,\chi_{0} \]

\[ |\psi_{-1}\rangle = \Psi_A(1,2)\,\chi_{-1} \]

Singlet state (\(S=0\), antisymmetric spin)

Must pair with the symmetric spatial part \(\Psi_S(1,2)\).

• Spin function:

\[ \chi_{\text{singlet}} = \frac{1}{\sqrt{2}}\!\left[\alpha(1)\beta(2) - \beta(1)\alpha(2)\right] \]

• Total wavefunction:

\[ |\psi_{\text{singlet}}\rangle = \Psi_S(1,2)\,\chi_{\text{singlet}} \]

Action of Spin Operators

Triplets:

\[ \hat{S}_z|\psi_{+1}\rangle = +\hbar|\psi_{+1}\rangle,\quad \hat{S}_z|\psi_{0}\rangle = 0,\quad \hat{S}_z|\psi_{-1}\rangle = -\hbar|\psi_{-1}\rangle \]

\[ \hat{S}^2|\psi_{+1,0,-1}\rangle = 2\hbar^2|\psi_{+1,0,-1}\rangle \]

Singlet:

\[ \hat{S}_z|\psi_{\text{singlet}}\rangle = 0,\qquad \hat{S}^2|\psi_{\text{singlet}}\rangle = 0 \]

Which is lower in energy?

• Triplet has electrons spatially antisymmetric → they avoid each other → less Coulomb repulsion → lower energy

• Singlet is spatially symmetric → electrons more overlapping → higher energy

• This is the origin of exchange stabilization.

Energies of Multi-Electron States

The Hamiltonian is

\[ \hat{H} = \hat{H}_1 + \hat{H}_2 + \hat{H}_{12}, \]

with \(\hat{H}_{12}\) corresponding to electron–electron repulsion.

Useful Integrals

Single-electron energy

\[ I(a) = \int \phi_a^*(r) \left[ -\frac{\hbar^2}{2m}\nabla^2 - \frac{Ze^2}{4\pi\epsilon_0 r} \right] \phi_a(r)\, d\tau \]

Coulomb Integral

\[ J_{ij} = \int |\phi_i(r_1)|^2 \frac{e^2}{4\pi\epsilon_0 r_{12}} |\phi_j(r_2)|^2 , d^3r_1, d^3r_2, \]

always positive.

Exchange Integral

\[ K_{ij} = \int \phi_i^*(r_1)\phi_j^*(r_2) \frac{e^2}{4\pi\epsilon_0 r_{12}} \phi_j(r_1)\phi_i(r_2), d^3r_1, d^3r_2. \]

Positive, but leads to energy lowering for triplet states.

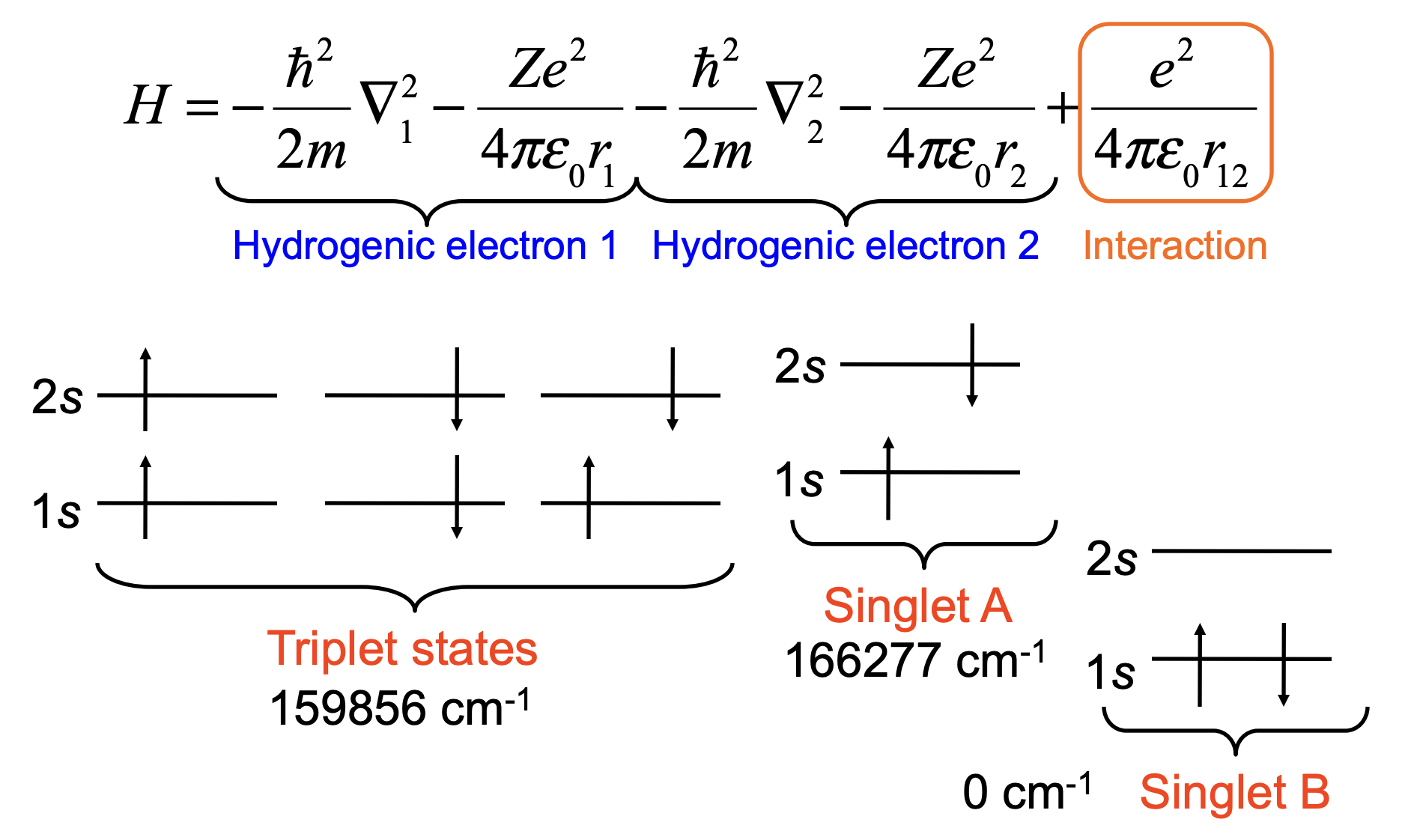
Energies of \(1s2s\) Singlet and Triplet

Triplet (antisymmetric spatial):

\[ E_{\text{triplet}} = I(1s) + I(2s) + J(1s,2s) - K(1s,2s) \]

Singlet (symmetric spatial):

\[ E_{\text{singlet}} = I(1s) + I(2s) + J(1s,2s) + K(1s,2s) \]

Thus the triplet state is lower in energy due to exchange stabilization.

Hund’s Rule and the Aufbau Principle

Fig. 91 Aufbau filling pattern for atomic orbitals.

Aufbau Principle

Electrons fill orbitals in order of increasing energy.

Pauli Exclusion Principle

Each orbital holds at most two electrons with opposite spins.

Hund’s Rule

Electrons occupy degenerate orbitals singly with parallel spins before pairing. This reflects exchange stabilization.

Fig. 92 Exchange stabilization in the triplet state underlies Hund’s rule.