BO approximation#
What you need to know
Born-Oppenheimer (BO) approximation, Because nuclei are much heavier than electrons, the Schrodinger equation can be approximately separated into the nuclear and the electron parts. Thus the electronic Schrodinger equation for a molecule can be solved separately at each fixed nuclear configuration. This is called the Born-Oppenheimer approximation.
BO approximation allows us to extend multi-electron treatment of atoms to molecules.
Single electron wavefunctions of molecules are called Molecular Orbitals (MO)
Geometry of \(H_2\) molecule defined by its bond length \(R\) is fixed when determining molecular orbitals.
Nuclear geometry is a varyable parameter in the problem: For different values of R one gets different energies and MOs.
Simplest molecule#
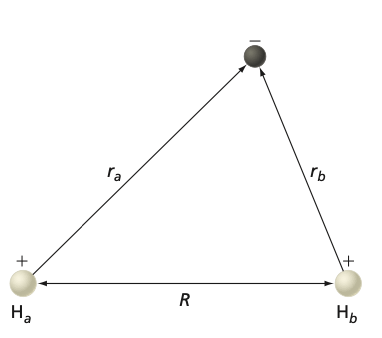
Fig. 99 Coordinates used to describe \(H^{+}_2\) molecule.#
In the following, we will consider the simplest molecule \(H_2^+\), which contains only one electron. This simple system will demonstrate the basic concepts in chemical bonding. The Schr”odinger equation for H\(_2^+\) is:
where \(\vec{r}_1\) is the vector locating the (only) electron and \(\vec{R}_A\) and \(\vec{R}_B\) are the positions of the two protons. The Hamiltonian for H\(_2^+\) is:
where \(M\) is the proton mass, \(m_e\) is the electron mass, \(r_{1A}\) is the distance between the electron and nucleus A, \(r_{1B}\) is the distance between the electron and nucleus B and \(R\) is the A - B distance.
Note that the Hamiltonian includes also the quantum mechanical kinetic energy for the protons. As such the wavefunction depends on \(\vec{r}_1\), \(\vec{R}_A\) and \(\vec{R}_B\).
The BO approximation#
Fig. 100 Max Born#
Fig. 101 Robert J Oppenheimer#
Because the nuclear mass \(M\) is much larger than the electron mass \(m_e\), the wavefunction can be separated (Born-Oppenheimer approximation):
where \(\psi_e\) is the electronic wavefunction that depends on the distance \(R\) between the nuclei and \(\psi_n\) is the nuclear wavefunction depending on \(\vec{R}_A\) and \(\vec{R}_B\). It can be shown that the nuclear part can be often be separated into vibrational, rotational and translational parts. The electronic Schr”odinger equation can now be written as:
Note that equation depends parametrically on \(R\) (``one equation for each value of \(R\)’’). The electronic Hamiltonian is:
Because \(R\) is a parameter, both \(E_e\) and \(\psi_e\) are functions of \(R\).