DEMO: Quantum Waves

import numpy as np
import matplotlib.pyplot as plt
from ipywidgets.widgets import interact, interactive

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

Linear superspositions and time dependence

def psi_n(x, n):
    """Time-independent wavefunction for a particle in a box."""
    L = 1 # set box length

    return np.sqrt(2/L) * np.sin(n * np.pi * x / L)

def T_n(t, n):
    """Time dependence factor for the wavefunction."""
    L = 1 # set box length
    m, hbar = 1, 1 # set atomic units
    En = n**2 * np.pi**2 * hbar**2 / (2 * m * L**2)

    return np.exp(-1j * En * t / hbar)

def psi_combined(x, t, L, c1=1, c2=1, n1=1, n2=2):
    """Time-dependent wavefunction for a linear superposition of two states of PIB"""

    return c1 * psi_n(x, n1) * T_n(t, n1) + c2 * psi_n(x, n2) * T_n(t, n2)

Plot time dependent quantum wavefunctions

def plot_wavefunction(t=0, c1=1, c2=1, n1=1, n2=1):

    L = 1.0
    x = np.linspace(0, L, 1000)

    psi_squared_x = np.abs(psi_combined(x, t, c1, c2, n1, n2))**2

    plt.plot(x, psi_squared_x )

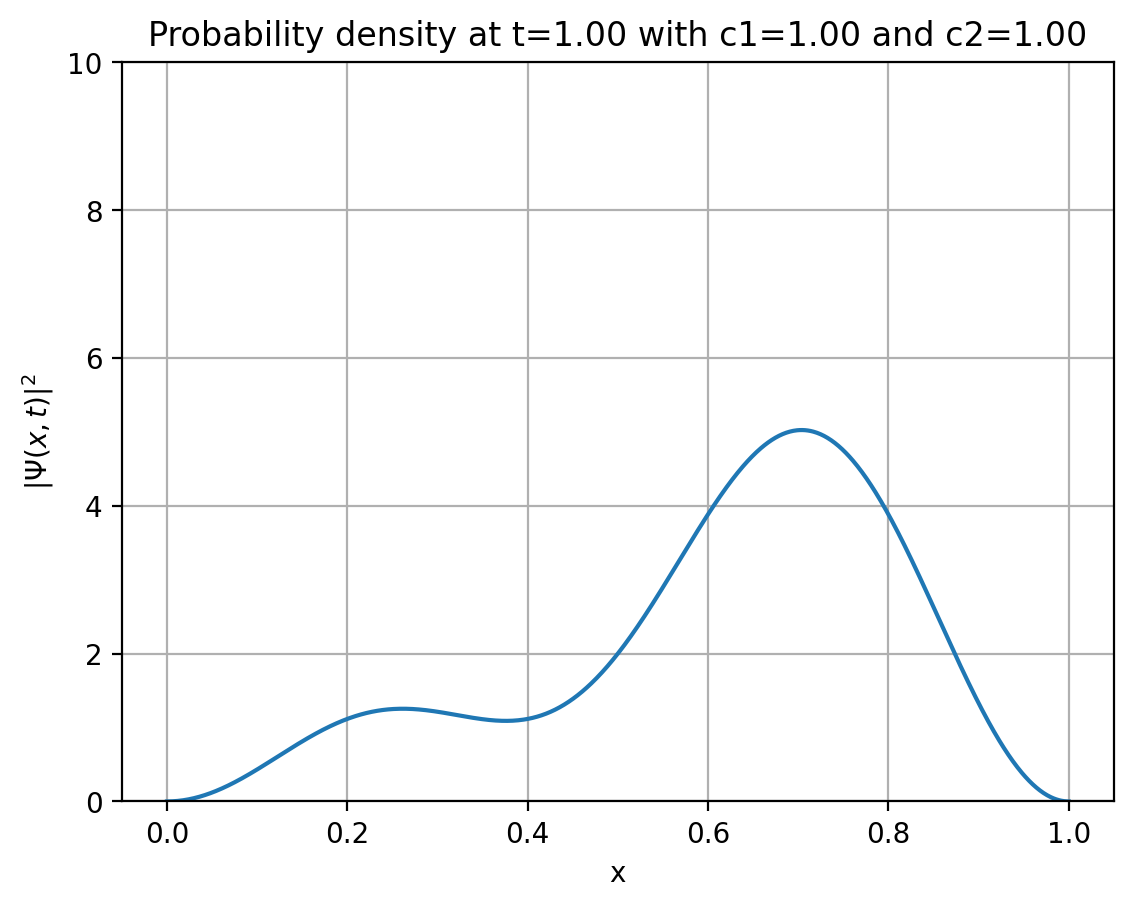
    plt.title(f"Probability density at t={t:.2f} with c1={c1:.2f} and c2={c2:.2f}")
    plt.xlabel('x')
    plt.ylabel('$|\Psi(x, t)|^2$')
    plt.grid(True)
    plt.ylim([0, 10])  # Adjust the y limit to suit the range of the probability density
    plt.show()

plot_wavefunction(t=1, c1=1, c2=1, n1=1, n2=1)

interact(plot_wavefunction, t=(0, 10, 0.1), c1=(-1.5, 1.5, 0.1), c2=(-1.5, 1.5, 0.1), n1=(1,5), n2=(1,5))

<function __main__.plot_wavefunction(t=0, c1=1, c2=1, n1=1, n2=1)>