DEMO: Visualizing waves

Show code cell source Hide code cell source

#@title Import libs

import numpy as np  
import matplotlib.pyplot as plt
import ipywidgets
from ipywidgets import interact, interactive, Dropdown
from matplotlib.animation import FuncAnimation
from IPython.display import HTML

import plotly.graph_objects as go
from plotly.subplots import make_subplots

%matplotlib inline
%config InlineBackend.figure_format='retina'

try:
    from google.colab import output
    output.enable_custom_widget_manager()
    print('All good to go')
except:
    print('Okay we are not in Colab just proceed as if nothing happened')

Okay we are not in Colab just proceed as if nothing happened

Standing and traveling waves in 1D

We begin by plotting a simple periodic function using numpy and matplotlib

\[y = \sin(kx)=\sin\left(\frac{2\pi}{\lambda} x\right)\]

Here are the main steps:

• Generate grid of points for x (lets say 1000 equiditant points between 0 and 1)

• Calcualte y values on this grid points

• Plot y vs x

# Generate 1000 points between 0 and 1 for the x-axis
x = np.linspace(0.0, 1.0, 1000)

# Calculate the y-values based on the sine wave formula
L = 1 # specify wavelength
y = np.sin(2 * np.pi * x / L)

# Create the plot
plt.plot(x, y, label=f'L = {L}')

[<matplotlib.lines.Line2D at 0x7fb2d4844b20>]

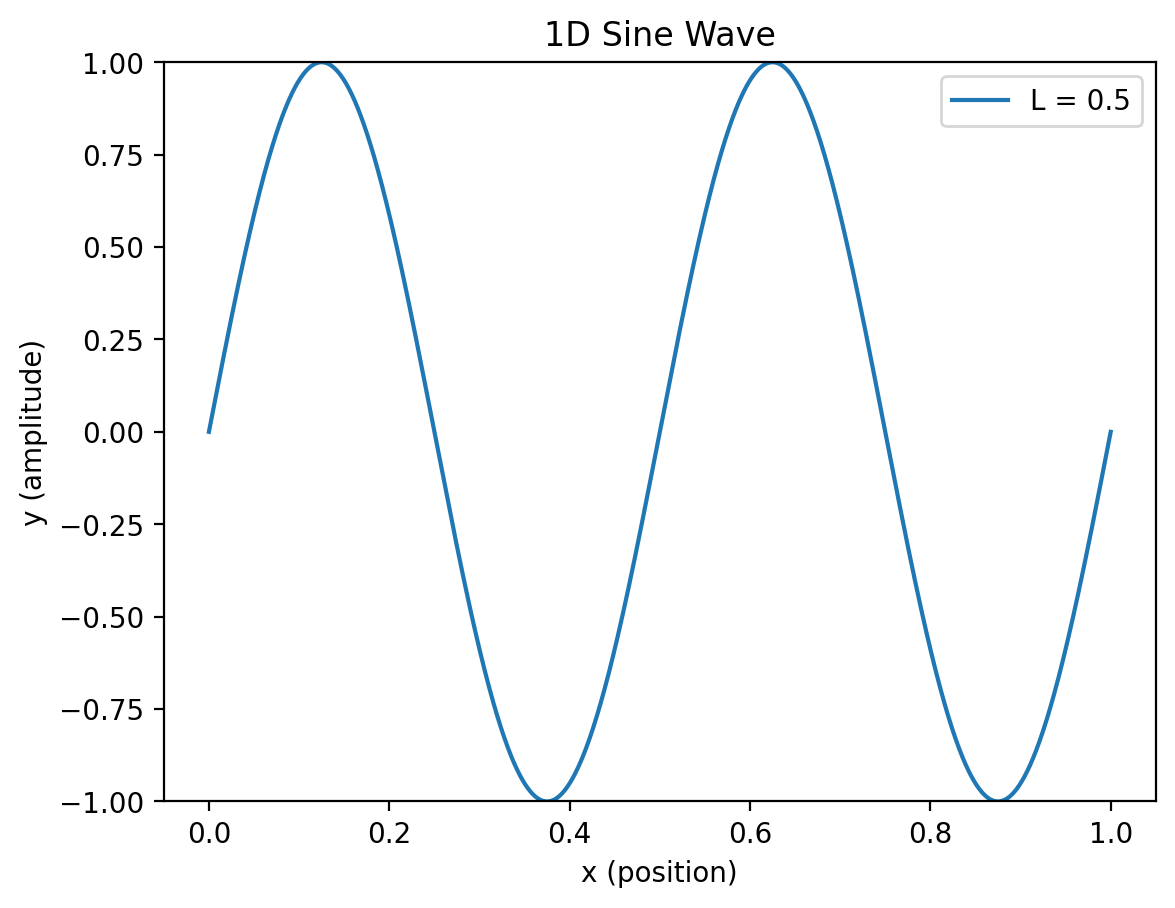
Now lets package this into a nice little function so we can reuse it in animations!

Show code cell source Hide code cell source

def wave1d(L=2):
    """
    Plots a 1D sine wave with a specified wavelength.

    Parameters:
    L (float): Wavelength of the sine wave. Default is 2 units.

    The function generates a sine wave of the form y = sin(2πx / L) and 
    plots it over the domain x = [0, 1]. The plot includes labeled axes, 
    a title, and a legend showing the value of L (wavelength).
    """
    
    # Generate 1000 points between 0 and 1 for the x-axis
    x = np.linspace(0.0, 1.0, 1000)
    
    # Calculate the y-values based on the sine wave formula
    y = np.sin(2 * np.pi * x / L)

    # Create the plot
    plt.plot(x, y, label=f'L = {L}')
    
    # Label the axes
    plt.xlabel('x (position)')
    plt.ylabel('y (amplitude)')
    
    # Add a title and legend
    plt.title('1D Sine Wave')
    plt.legend()
    
    # Set limits for the y-axis to improve clarity
    plt.ylim(-1, 1)
    
    # Display the plot
    plt.show()

# Change wavelength
wave1d(L=0.5)

Making wave functions interactive

• By adding @widgets.interact(parameters=(init,final)) to our functions we can interactively parameters in the function using slider widgets.

interactive(wave1d, L=(0.1, 2))

Traveling, standing waves and wave interference

• The function generates two waves, wave1 and wave2, and their superposition.

• The waves are of the form \(y = sin(k(x - vt))\) and \(y = sin(k(x - vt) + \phi)\).

• where \(\phi\) is the phase shift between the two. All three waveforms are plotted on the same graph.

Show code cell source Hide code cell source

def wavef2(k=10, t=0, phi=0, v=1):
    """
    Plots two traveling waves and their superposition.

    Parameters:
    k (float): Wave number (related to wavelength). Default is 10.
    t (float): Time at which to evaluate the wave. Default is 0.
    phi (float): Phase shift between the two waves. Default is 0.
    v (float): Velocity of the waves. Positive velocity moves the wave to the right. 
               Try flipping the direction of velocity (negative v) to observe standing waves.
    """
    
    # Create 1000 points between 0 and 1 for the x-axis
    x = np.linspace(0, 1., 1000)
    
    # Define the first traveling wave
    wave1 = np.sin(k * (x - v * t)) 
    
    # Define the second traveling wave with a phase shift
    wave2 = np.sin(k * (x - v * t) + phi)  # Flip v to observe a standing wave effect
    
    # Plot the two individual waves and their superposition
    plt.plot(x, wave1, lw=2, color='blue', label='Wave 1')
    plt.plot(x, wave2, lw=2, color='green', label='Wave 2')
    plt.plot(x, wave1 + wave2, lw=3, color='red', label='Wave 1 + Wave 2')
    
    # Set limits for the y-axis
    plt.ylim([-2.5, 2.5])
    
    # Add a legend and grid for clarity
    plt.legend()
    plt.grid(True)
    
    # Display the plot
    plt.show()

interactive(wavef2, k=(2, 20), t=(0,50.0,0.1), phi=(0, 2*np.pi, np.pi/8),v=1)

Show code cell source Hide code cell source

#@title Animate traveling wave in 3D

def wave_x_t(A=1, k=1.0, omega=1, phi=0):
    # Create a grid of x and t values
    x = np.linspace(0, 2 * np.pi, 100)
    t = np.linspace(0, 2 * np.pi, 100)
    X, T = np.meshgrid(x, t)

    # Calculate the wave amplitude for each combination of x and t
    Y = A * np.sin(k * X - omega * T + phi)

    # Create the figure
    fig = go.Figure(
        data=[go.Surface(z=Y, x=X, y=T, colorscale='Viridis')],
        layout=go.Layout(
            title='Traveling Wave Animation',
            scene=dict(
                xaxis_title='Position',
                yaxis_title='Time',
                zaxis_title='Amplitude',
                camera_eye=dict(x=1.5, y=1.5, z=1.5),
            ),
            width=800,
            height=800,
            updatemenus=[dict(type='buttons', showactive=False,
                              buttons=[dict(label='Play',
                                             method='animate',
                                             args=[None, dict(frame=dict(duration=50, redraw=True), 
                                                              mode='immediate')])])]
        )
    )

    # Generate frames for the animation
    frames = []
    for phi in np.linspace(0, 2 * np.pi, 100):
        Y = A * np.sin(k * X - omega * T + phi)
        frames.append(go.Frame(data=[go.Surface(z=Y, x=X, y=T)], name=str(phi)))

    fig.frames = frames

    return fig

# Generate and show the animation
fig = wave_x_t(A=1, k=1.0, omega=1, phi=0)
fig.show()

Normal modes of 1D guitar string

Show code cell source Hide code cell source

def guitar1d(n=1, t=0):
    """
    Visualizes the 1D normal mode of a vibrating guitar string at a specific time.

    Parameters:
    n (int): Mode number (harmonic) of the vibrating string. Default is 1.
    t (float): Time at which to evaluate the normal mode. Default is 0.
    
    The function plots the displacement of the string at time t based on the 
    normal mode solution y(x, t) = sin(n * pi * x / L) * cos(omega * t), where
    L is the length of the string (default is 1) and omega is the angular frequency.
    """
    
    # Constants
    v = 1          # Wave speed
    L = 1          # Length of the string
    omega = np.pi * v / L  # Angular frequency for the fundamental mode (n=1)
    
    # Spatial grid from 0 to L
    x = np.linspace(0, L, 1000)
    
    # Compute the displacement of the string for mode n and time t
    y = np.sin(n * np.pi * x / L) * np.cos(omega * t)
    
    # Plot the displacement of the string
    plt.plot(x, y, lw=3)
    
    # Add title, grid, and axis limits
    plt.title(f'Normal Mode #{n} of a 1D Guitar String')
    plt.grid(True, linestyle='--')
    plt.ylim(-1, 1)
    
    # Label the axes
    plt.xlabel('Position along string (x)')
    plt.ylabel('Displacement (y)')
    
    # Display the plot
    plt.show()

interactive(guitar1d, n=(1,10), t=(0, 10, 0.1))

1D guitar vibrations as linear combination of normal modes

\[u(x,t) = c_1 u_1 + c_2 u_2 +c_3 u_3 + ...\]

• \(u_n = sin(n \pi x / L) \cdot cos(n \pi v t / L)\), normal modes

• \(c_n=0-1\) coeficients of modes

Show code cell source Hide code cell source

#@title Animate mode combinations

def create_animation(modes, coefficients):
    # Parameters
    v = 1  # wave speed
    L = 1  # length of the string

    # Set up the figure and axis
    fig, ax = plt.subplots(figsize=(10, 5))
    x = np.linspace(0, L, 500)  # Reduce resolution to 500 points
    line, = ax.plot(x, np.zeros_like(x), lw=3)
    ax.set_ylim(-1.5, 1.5)

    # Update title to include selected modes
    modes_str = ', '.join(map(str, modes))
    ax.set_title(f"Combination of Normal Modes: {modes_str}")
    ax.set_xlabel("Position along the string (x)")
    ax.set_ylabel("Displacement (y)")
    ax.grid('--')

    # Animation function
    def update(frame):
        t = frame / 10  # Adjust time scaling
        y = sum(c * np.sin(n * np.pi * x / L) * np.cos(n * np.pi * v * t / L) 
                 for n, c in zip(modes, coefficients))
        line.set_ydata(y)
        return line,

    # Create the animation
    ani = FuncAnimation(fig, update, frames=np.arange(0, 50), interval=100, blit=True)  # Reduced to 50 frames
    plt.close(fig)  # Prevents static display of the last frame
    return HTML(ani.to_jshtml())

modes = [1, 2, 3]       # Change mode  numbers (from 1 to 10)
coefficients = [1, 1, 1] # Change their coefficients (from 0-1)

create_animation(modes, coefficients)

Once Loop Reflect

Normal modes of a 2D membrane

Show code cell source Hide code cell source

def membrane2d_mode(n=1, m=1, t=0):
    """
    Calculates the 2D grid of points (X, Y) and the normal mode displacement (Z) of a vibrating 
    rectangular membrane at a specific time t.

    Parameters:
    n (int): Mode number along the x-direction. Default is 1.
    m (int): Mode number along the y-direction. Default is 1.
    t (float): Time at which to evaluate the normal mode. Default is 0.

    Returns:
    X, Y, Z (numpy arrays): Grid of points in the X-Y plane and the corresponding 
                            membrane displacement Z(X, Y, t).
    """
    
    # Constants
    Lx, Ly = 1.0, 1.0  # Dimensions of the rectangular region
    v = 0.1            # Wave speed 
    omega = v * np.pi / Lx * (n**2 + m**2)  # Angular frequency for the normal mode
    
    # Create a spatial grid
    Nx, Ny = 100, 100  # Number of grid points in each dimension
    x, y = np.linspace(0, Lx, Nx), np.linspace(0, Ly, Ny)
    X, Y = np.meshgrid(x, y)

    # Compute the spatial part of the normal mode
    Z = np.sin(m * np.pi * X / Lx) * np.sin(n * np.pi * Y / Ly) * np.cos(omega * t)
    
    return X, Y, Z

def viz_membrane2d_plotly(n=1, m=1, t=0): 
    """
    Visualizes the 2D normal modes of a vibrating membrane on a square geometry using Plotly.
    
    This function displays both a 2D contour plot and a 3D surface plot of the membrane displacement.

    Parameters:
    n (int): Mode number along the x-direction. Default is 1.
    m (int): Mode number along the y-direction. Default is 1.
    t (float): Time at which to evaluate the normal mode. Default is 0.
    """
    
    # Get the membrane displacement at time t
    X, Y, Z = membrane2d_mode(n, m, t)
    
    # Create a Plotly subplot with 2 views: 2D contour and 3D surface
    fig = make_subplots(
        rows=1, 
        cols=2, 
        subplot_titles=('2D Contour Plot', '3D Surface Plot'),
        specs=[[{"type": "contour"}, {"type": "surface"}]]
    )
    
    # Add 2D contour plot to the left side
    fig.add_trace(
        go.Contour(x=X.flatten(), y=Y.flatten(), z=Z.flatten(), colorscale='RdBu'),
        row=1, col=1
    )

    # Add 3D surface plot to the right side
    fig.add_trace(
        go.Surface(x=X, y=Y, z=Z, colorscale='RdBu'),
        row=1, col=2
    )

    # Update the layout for better visualization
    fig.update_layout(
        title_text="2D Contour and 3D Surface Plots of Membrane Vibrational Normal Modes",
        width=1000,
        height=500
    )
    
    # Show the figure
    fig.show()

interact(viz_membrane2d_plotly, n=(1,1), m=(2,3), t=(0,100))

<function __main__.viz_membrane2d_plotly(n=1, m=1, t=0)>