DEMO: Bonus challenge#

Quantum Waves

Prerequisites

How to complete the work

  • Run the cell below to import all necessary libraries.

  • Add code below each problem.

  • Run the code in Google Collab then download the file either as *.ipynb or *py file.

  • Submit your file to Canvas.

  • Do not forget that Google Collab deletes files if you do not save them iin your Google Drive.

import numpy as np
import matplotlib.pyplot as plt
from ipywidgets.widgets import interact, interactive

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

Problem 1: Time independent PIB#

Evaluate the following quantities using particle in a box wavefunctions

  • Most likely to be in the middle thrid of box

  • Average momentum and momentum square

  • Average position and position square

  • Show uncertainty relation

Hint: For some averages you may want to take numerical derivatives. Below is an example on how to do it using grad function of numpy. Also recall that numerically integral is just a sum over small discretized space dx. This is done by trapz function of numpy which is using trapezoidal rule

from  numpy import gradient as grad 
from numpy import trapz 

### Define boundaries and dx-
L  = 1
N  = 1000
dx = L/N
x  = np.linspace(0, L, N)

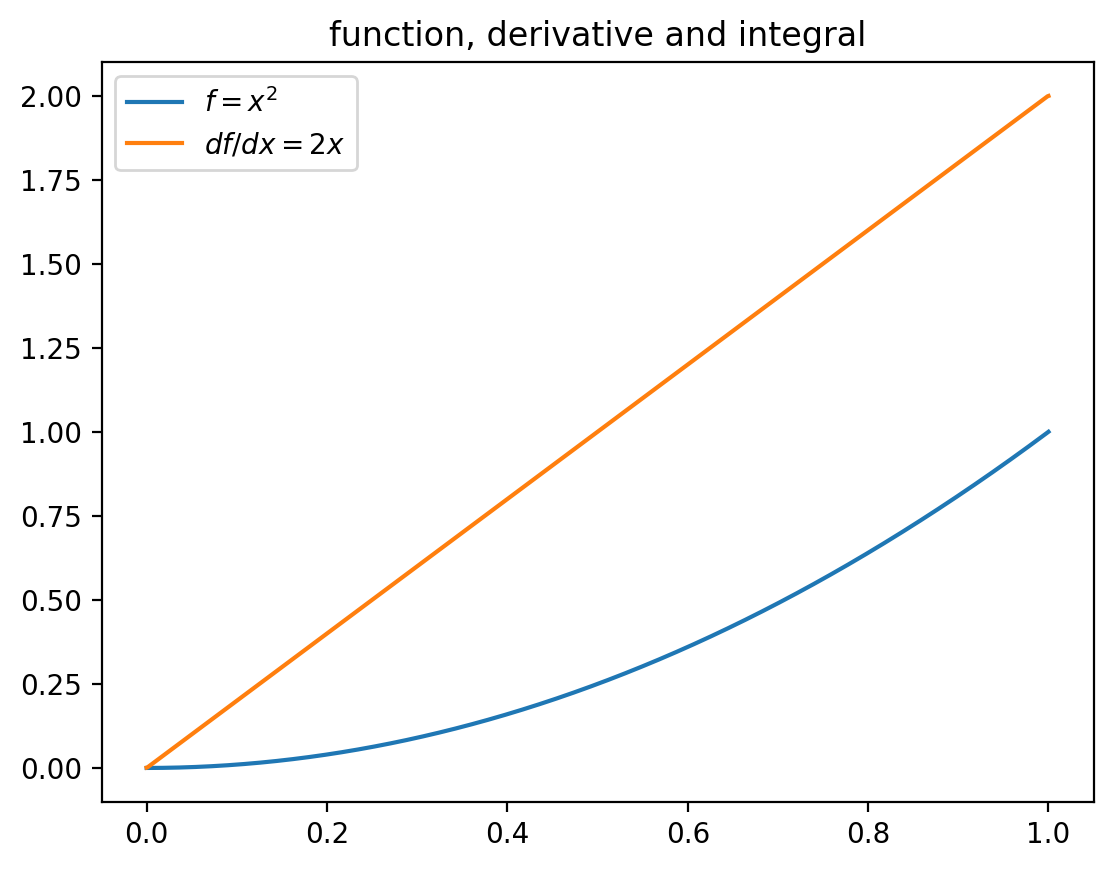
### A numerical array of function. Feel free to change this function, e.g exp or sine etc
f = x**2

plt.plot(x, f, label=r'$f=x^2$')

### First derivative function f(x)
dfdx = grad(f, x)

plt.plot(x, dfdx, label=r'$df/dx=2x$')

### Compute integral now using trapezoidal rule
int_f = np.trapz(dfdx, dx=dx)
print('Numerical integral:', int_f)

plt.legend()
plt.title('function, derivative and integral')

Numerical integral: 0.999

Text(0.5, 1.0, 'function, derivative and integral')
../_images/3dfebe054c9e2be71b52d25e8a3ec33b118c673fd3b90e43e3da87e83fee61ef.png

Problem 2: Time dependent PIB#

  • Compute time dependence of average position of a particle in a box as a linear combination of first two states weights.

  • Show the effect of changing second state into more excited states

Problem 3: Fourier transform and QM#

  • Fourier transform position wavefunction \(\psi(x)= \frac{1}{(2\pi \sigma^2)^{1/2}}\frac{}{}e^{-x^2/(2\sigma^2_x)}\) which will give you momentum wavefunction \(\psi(p)\).

  • Show uncertainty relation by varying sigma=0.1, 1, 10

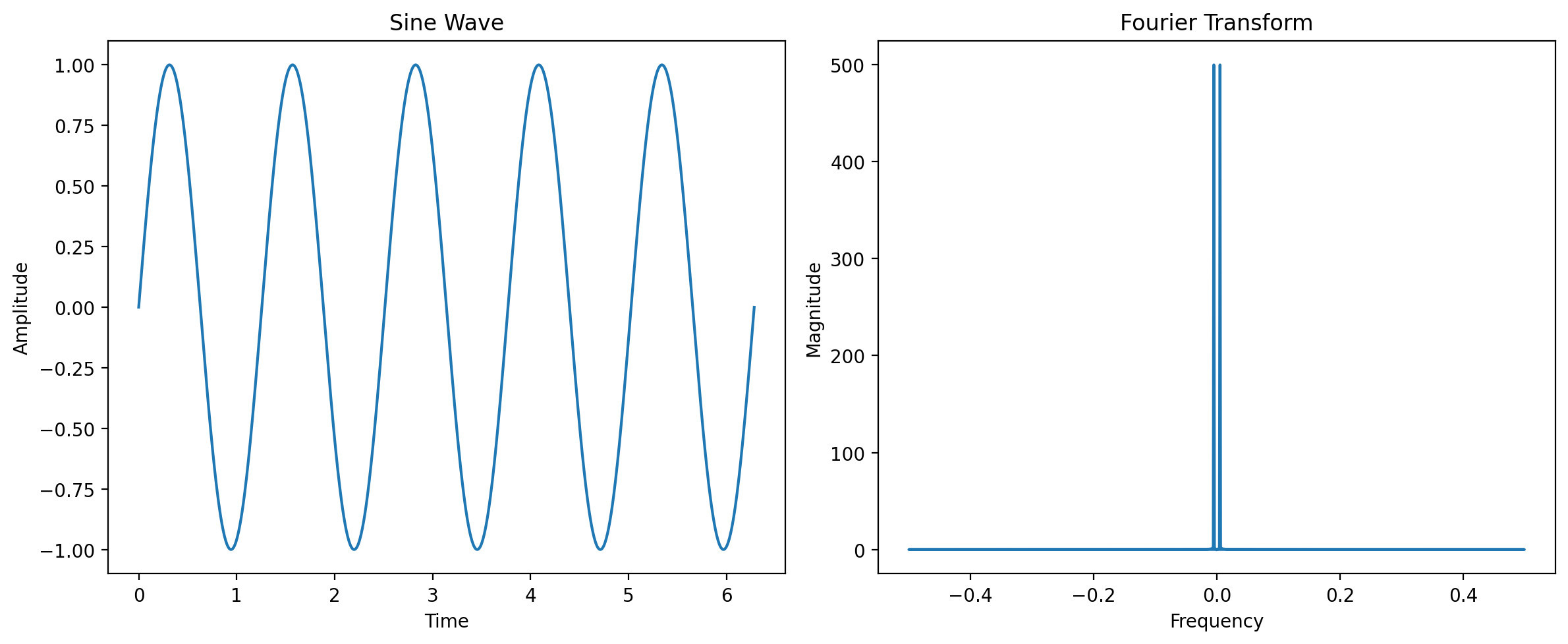
Below are two examples of Fourier transform

# Create a sine wave
x = np.linspace(0, 2*np.pi, 1000)
y = np.sin(5*x)

# Compute Fourier transform
Y = np.fft.fft(y)
frequencies = np.fft.fftfreq(len(Y))

# Plot
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(x, y)
plt.title('Sine Wave')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.subplot(1, 2, 2)
plt.plot(frequencies, np.abs(Y))
plt.title('Fourier Transform')
plt.xlabel('Frequency')
plt.ylabel('Magnitude')
plt.tight_layout()
plt.show()
../_images/49565e3cff71b9dadda9ddb9e78c9adcb55a9fe6b872706265dfbce096ac3d6d.png 
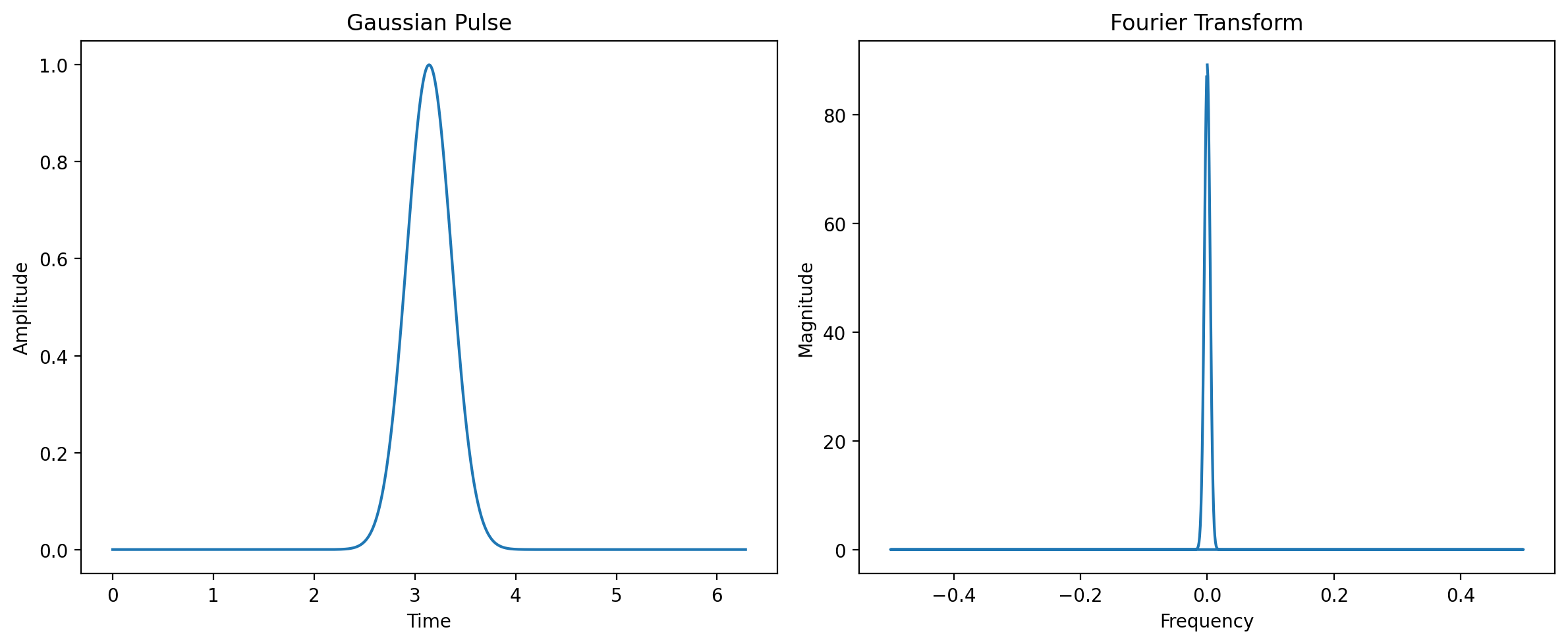
# Create a Gaussian pulse
y3 = np.exp(-(x-np.pi)**2/0.1)

# Compute Fourier transform
Y3 = np.fft.fft(y3)

# Plot
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(x, y3)
plt.title('Gaussian Pulse')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.subplot(1, 2, 2)
plt.plot(frequencies, np.abs(Y3))
plt.title('Fourier Transform')
plt.xlabel('Frequency')
plt.ylabel('Magnitude')
plt.tight_layout()
plt.show()
../_images/f6ce7bd03b54eaf866af13544cc32fe2e4a2222565df705c122d8b827900fe07.png