P1 Characteristics of Quantum Wavefunctions#
What you need to know
The finite depth box is a more realistic model compared to the infinite potential well, as it allows for the possibility of quantum tunneling, where the particle has a non-zero probability of being found outside the well.
The potential energy function is finite in the central region and zero outside. The time-independent Schrödinger equation is solved in three regions, with different forms of wavefunctions in each. - Bound states are possible due to the confinement of the particle, but the energy levels are determined by matching the wavefunction and its derivative at the boundaries, leading to transcendental equations.
Unlike the infinite well, the number of bound states is finite, and the wavefunctions extend slightly outside the well, illustrating the quantum tunneling effect.
Understanding the boundary conditions and the behavior of the wavefunctions in each region is key to solving this problem.
Acknowledgement
These Jupyter notebooks is based on the excellent paper by J Chem. Educ. 2019, 96, 8, 1663–1670
Quantum objects can go where no classical partciles are allowed!#
Qualitative trends in wavefunction beahviour#

Fig. 53 Example of a stepped potential and expected behaviour of the wavefunction.#
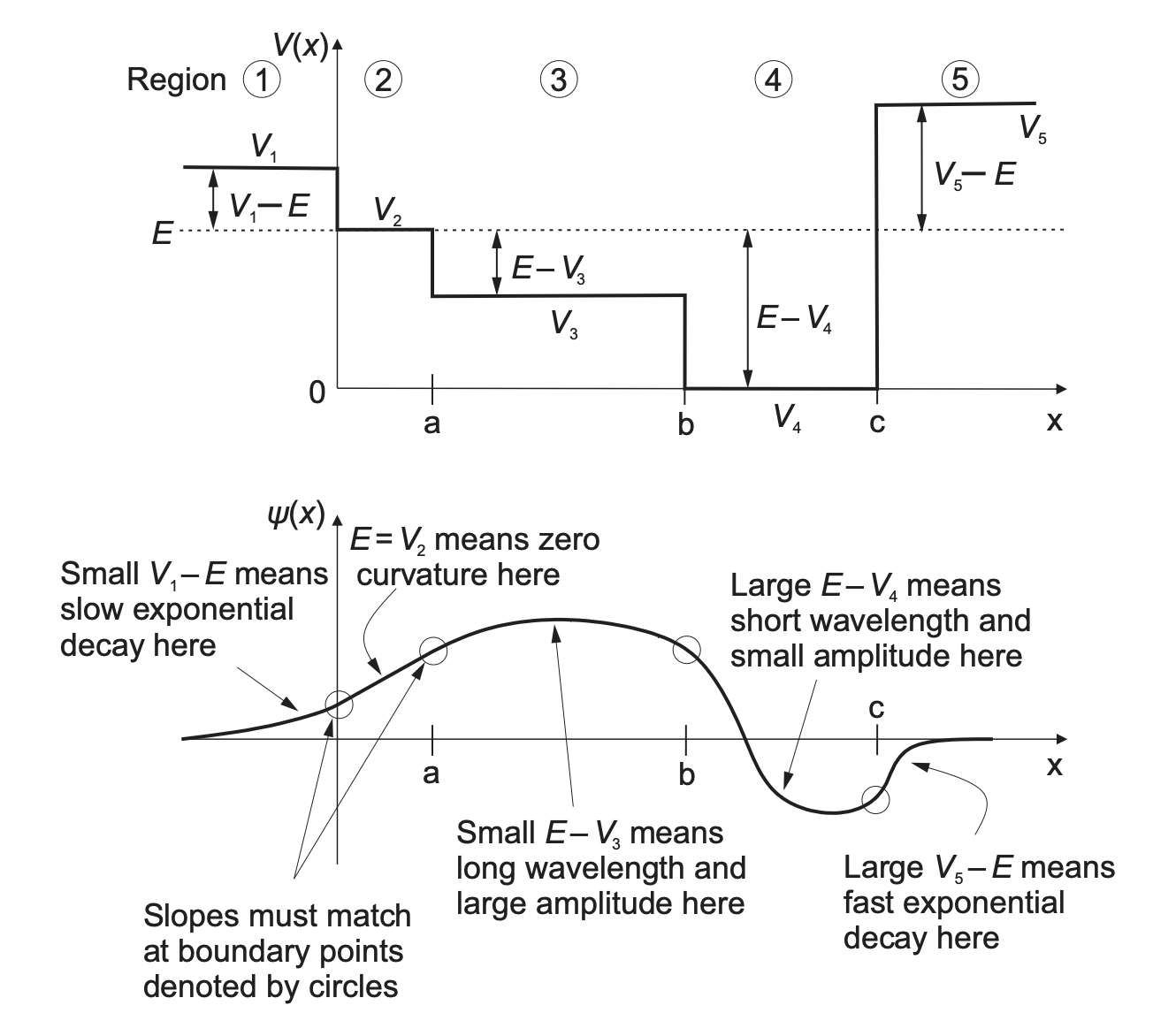
Fig. 54 Judging by the signs of the various terms of schrodinger equation we can predict qualtiatively how wavefunction would beahave.#
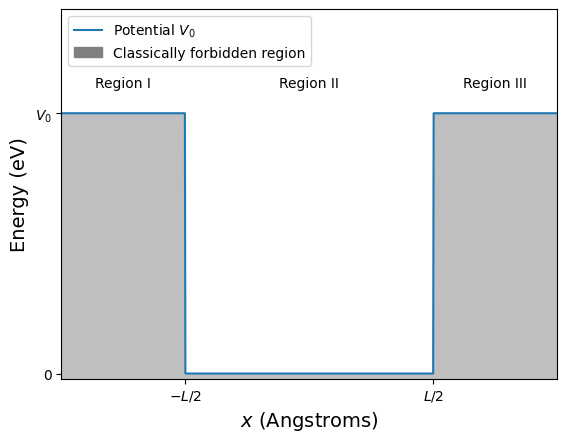
Solutions inside square well#
Inside the finite square well, the region \(-L/2 \le x \le L/2\), the potential \(V(x)=0\) so the Schrödinger equation,
Solutions to this equations have the form showing oscillatory profile for wavefunction
Solutions outside the well#
In the regions where \(x < -L/2\) and \(x > L/2\), the potential is \(V(x) = V_0\). The time-independent Schrödinger equation for these regions can be written as:
where \(k^2 = \frac{2m(V_0 - E)}{\hbar^2}\). The value of \(k\) will differ in each region of the potential well depending on the energy and potential.
What happens when \(E < V_0\)?
When the particle’s energy is less than the potential outside the well \((E < V_0)\), the term \(E - V_0\) becomes negative. This makes \(k^2 = \frac{2m(V_0 - E)}{\hbar^2}\), which means \(k\) is real, and the solution in this region involves an exponential decay (i.e., evanescent wave). Therefore, \(k\) is no longer purely imaginary, and the wavefunction decays exponentially as the particle penetrates into the classically forbidden regions outside the well.
Profile of the full wavefunction#
Our potential well is composed of three regions and the particle will have an energy less than the potentail, i.e. \(E<V_0\). In order that the wavefunction can be normalised we make the following choices so that as \(x\rightarrow\pm\infty\) the value of \(\psi(x)\rightarrow 0\). We will also choose the trigonometic form of the wavefunction inside the potential, recall this is to make the maths easier.
Why do we check for continuity?
\(\psi^{'}\) needs to be continuous to guarantee the existence of \(\psi^{''}\), whose existence is required from the first postulate.
\(\large{\frac{d^2}{dx^2}}\) is a component of the kinetic energy operator. If the wavefucntion doesn’t have a well-defined second derivative, then the kinetic energy would be undefined, which is not possible.
Boundary conditions#
The wavefunction will be the sum of all three components so we make sure that the wavefunction and it’s first derivative are continuous at any boundary. We apply the following boundary conditions to achive this
note there are two conditions for each boundary so we will endup with 2 sets of 2 simultanious equations.
Even and odd solutions#
Finally, our potential is symmetric about \(x=0\) so our wavefunction will either be a maximum or zero at \(x=0\) so that the probability distribution is symmetric about \(x=0\). We will call these even for \(\psi(x)=\psi(x)\) and odd when \(\psi(x)=-\psi(-x)\).
Even solutions:
These are called even solutions because the function \(\cos(kx)\) is even, i.e. it is symmetric about \(x=0\). However, they will correspond to the odd values of \(n\).
After imposing the boundary conditions we reach the following relation:
Odd solutions:
These are called odd solutions because the function \(\sin(kx)\) is odd, i.e. it is anti-symmetric about \(x=0\). However, they will correspond to the even values of \(n\). This is a bit confusing I know but the choice of \(n\) is arbitrary! The sine and cosine solutions however are determined by the physics.
After imposing the boundary conditions we reach the following relation:
Unfortunately, we cannot find the allowed energies analytically. Instead we we have to chose either a graphically or numerically method.
What does that mean? We can graph the left and right hand side equations seperately as a function of energy \(E\) and look for the intersection points which will correspond to the allowed energy values (the energy eigen values).
Below I have plotted the functions for the odd and even wavefunctions using the Desmos graphing tool, you can adjust the potential \(V\) and the length \(L\), you can also click on the intercept points to determine the energy and value of the function.
Finding the energy eigen values graphically#
Here are some question to think about:
Q1: How does changing the width effect the number and energy of the states?
Q2: How does changing the potential effect the number and energy of the states?
Q3: Is the ground state described by an even or an odd wavefunction?
Q4: What is the minimum number of states?
Q5: Do the energy levels follow the same pattern as the infinite square well, i.e. \(E_n=E_1n^2\)?
Plots of the wavefunctions and prbability densities#
Now we know the energy eigen values we can use these to find expressions for the wavefunctions and probability densities. This may help you understand some of the choices we made up to this point. Take a look at the figure and consider again the choice of the wavefunction in the region I and III, and why we broke up the wavefunction into odd and even functions inside the well.
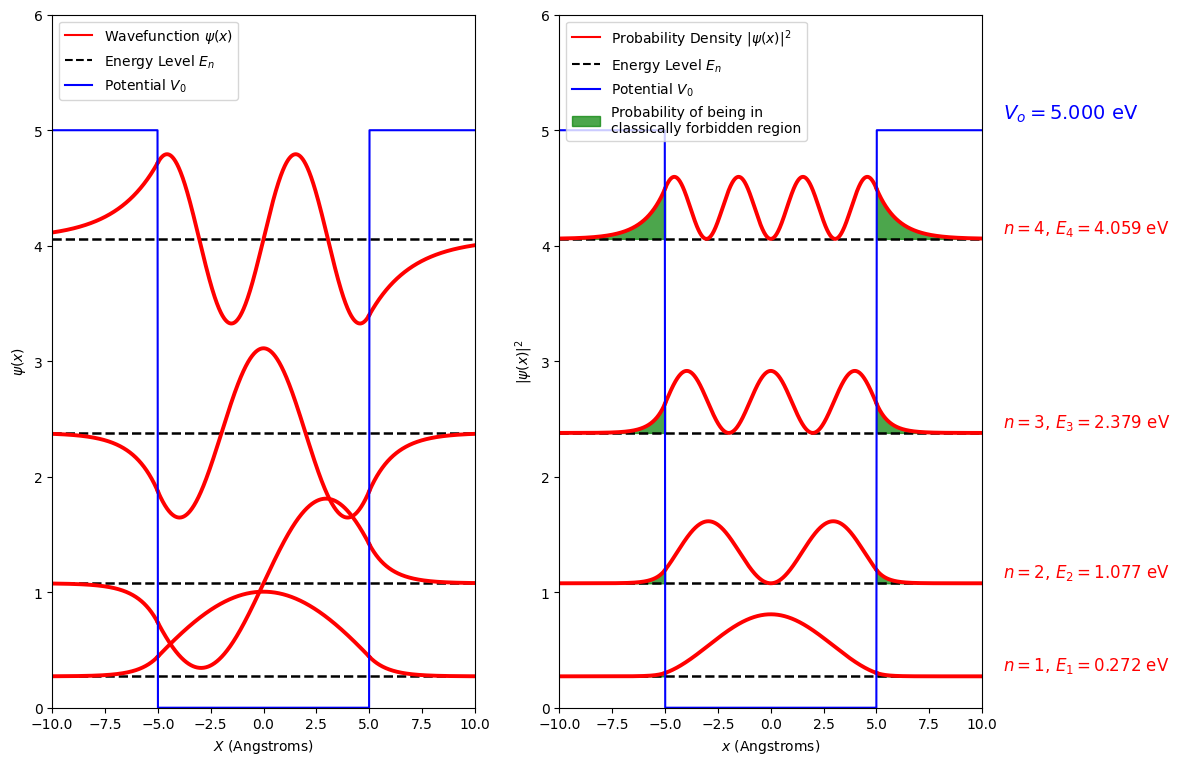
From these plots we can explain some of the behaviour of the energy levels as \(L\) and \(V_0\) are changed.
The first thing to note from the diagram above is that the wavefunction extend outside the potential, they enter what is sometime called the classically forbidden region.
As with the potential step the quantum description of the particle allows it to tunnel into a region where the potential is larger than the energy of the particle. This is indicated by the shaded green area in the probability density plot. Note, this gets larger as the value \(V_0-E\) approaches zero.
Tunneling of particle in the box#
The tunneling probability correspond to the area outside the box that has non-zero values of probability density. In the graphicaly representation, those areas are shaded in green. The integration of those areas provide the probability that the particle will tunnel outside the classically allowed region.
We can calculate \(P(-L/2>x>L/2)\), i.e. the size of the shaded green area, as a percentage of the total area:
The tunneling probabilities are:
State # 1 tunneling probability = 0.83%
State # 2 tunneling probability = 3.55%
State # 3 tunneling probability = 9.25%
State # 4 tunneling probability = 23.30%
A comparison between the energies of an infinite and finte square well#
These values show what we have already deduced, that the closer the state is to the top of the potential the easier it is to spread outside of the potential. How does this effect the energy levels? Lower in the potential the wavelength of the wavfunction is more closely related to the width of the potential than it is higher in the potential. Compare the same width potential for the infinite and finite square well below.
Notice that at energies closer to zero the infinite and finite energies are closer. As the energy of the state gets closer to the top of the finite potential it is smaller in the finite well than the infinite well. Why? The higher energy states allow the wavefunction in the finite squre well to spread out so the wavelength will be longer in the finite square well compared to the infinite squre well. - A longer wavelength corresponds to a smaller value of \(k\) (wavenumber) and hence a lower energy state.

