Hartree-Fock

Hartree-Fock#

Objective: Approximate the electronic structure of atoms and molecules by treating electrons as independent particles in an average field created by all other electrons.
Motivation: The Schrödinger equation for multi-electron systems is too complex to solve exactly.

Wavefunction#

The total wavefunction $Ψ (1, 2, \dots, N)$ is approximated as a single Slater determinant to satisfy the Pauli exclusion principle. $ $Ψ (1, 2, \dots, N) = \frac{1}{\sqrt{N!}} | \begin{matrix} ψ_{1} (1) & ψ_{2} (1) & \dots & ψ_{N} (1) \\ ψ_{1} (2) & ψ_{2} (2) & \dots & ψ_{N} (2) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ ψ_{1} (N) & ψ_{2} (N) & \dots & ψ_{N} (N) \end{matrix} |$ $

Hartree-Fock Equations#

Each molecular orbital (MO) $ψ_{i}$ satisfies the self-consistent field (SCF) equation: $ $\hat{F} ψ_{i} = ε_{i} ψ_{i}$ $w h e r e$ \hat{F} $i s t h e * * F o c k o p e r a t o r * * a n d$ \varepsilon_i$ are the orbital energies.

Fock Operator#

The Fock operator $\hat{F}$ is a sum of the one-electron Hamiltonian and a mean-field potential:

$\hat{F} = \hat{h} + \sum_{j} ({\hat{J}}_{j} - {\hat{K}}_{j})$
- $\hat{h}$ : Kinetic energy and nuclear attraction operators.
- ${\hat{J}}_{j}$ : Coulomb operator (electron-electron repulsion).
- ${\hat{K}}_{j}$ : Exchange operator (arises from antisymmetry requirement of the wavefunction).

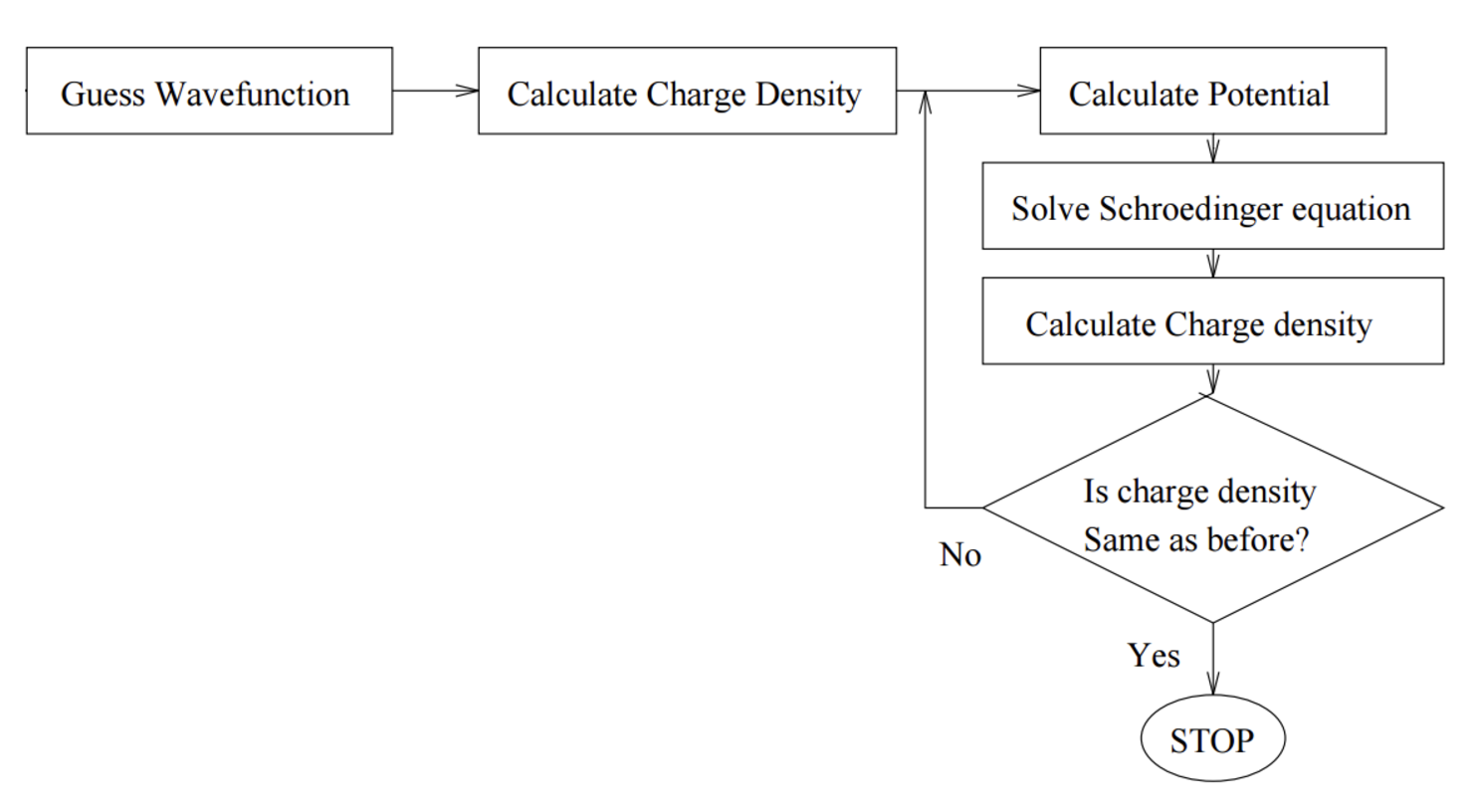
Self-Consistent Field (SCF) Method#

Guess initial molecular orbitals $ψ_{i}$ .
Construct the Fock operator $\hat{F}$ using the current $ψ_{i}$ .
Solve the Hartree-Fock equation $\hat{F} ψ_{i} = ε_{i} ψ_{i}$ to obtain new orbitals $ψ_{i}$ .
Repeat steps 2-3 until convergence (orbitals do not change significantly).

3. Total Energy of the System#

Total electronic energy $E_{H F}$ in the Hartree-Fock approximation:

$E_{H F} = \sum_{i} ⟨ ψ_{i} | \hat{h} | ψ_{i} ⟩ + \frac{1}{2} \sum_{i, j} (J_{i j} - K_{i j})$
- $J_{i j}$ : Coulomb integral.
- $K_{i j}$ : Exchange integral.

4. Strengths and Limitations#

Strengths#

Efficient: Reduces the complexity of the multi-electron Schrödinger equation.
Exchange interactions: Includes effects of exchange through the Slater determinant.

Limitations#

No dynamic correlation: Electron-electron correlation is only partially captured.
Post-Hartree-Fock methods: Needed for more accurate energy calculations (e.g., MP2, CCSD).

5. Summary#

Hartree-Fock approximates the multi-electron wavefunction as a Slater determinant.
The Fock operator accounts for one-electron and mean-field electron-electron interactions.
The SCF procedure ensures convergence to a consistent set of orbitals.
While efficient, it lacks dynamic correlation, motivating the development of post-Hartree-Fock methods.

Important Equations

Slater Determinant:

$\begin{array}{r} Ψ (1, 2, \dots, N) = \frac{1}{\sqrt{N!}} | \begin{array}{c} ψ_{1} (1) & ψ_{2} (1) & \dots & ψ_{N} (1) \\ ψ_{1} (2) & ψ_{2} (2) & \dots & ψ_{N} (2) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ ψ_{1} (N) & ψ_{2} (N) & \dots & ψ_{N} (N) \end{array} | \end{array}$
Hartree-Fock Equations:

$\hat{F} ψ_{i} = ε_{i} ψ_{i}$
Fock Operator:

$\hat{F} = \hat{h} + \sum_{j} ({\hat{J}}_{j} - {\hat{K}}_{j})$
Electronic Energy:

$E_{H F} = \sum_{i} ⟨ ψ_{i} | \hat{h} | ψ_{i} ⟩ + \frac{1}{2} \sum_{i, j} (J_{i j} - K_{i j})$

HF on example of He atom#

Practical use of HF#

We need to install a few things before we get started
- PySCF (for the quantum chemistry)
- py3DMol for visualizing the molecule
- plotly and kaleido for plotting

%pip install -q pyscf py3DMol plotly kaleido

Note: you may need to restart the kernel to use updated packages.

#@title PYSCF code to calcualte energies of Alkali Metals

from pyscf import gto, scf

# Function to calculate orbitals and energies for a given atom
def calculate_orbitals_energies(atom_symbol):
    """
    Calculate the orbitals and energies for a given atom using PySCF.
    
    Parameters:
    atom_symbol (str): Symbol of the atom (e.g., 'He', 'Li').
    
    Returns:
    dict: A dictionary containing the total energy, MO coefficients, and MO energies.
    """
    # Define the atom and basis set
    mol = gto.Mole()
    mol.atom = [(atom_symbol, (0, 0, 0))]  # Specify the atom and its position
    mol.basis = 'sto-3g'  # Basis set
    
    
    mol.spin = 1  # 2S = 1, since Li, Na, K has 1 unpaired electron
    
    mol.build()
    
    # Perform Hartree-Fock calculation
    mf = scf.RHF(mol)  # Restricted Hartree-Fock
    total_energy = mf.kernel()  # Calculate the total electronic energy
    
    # Extract molecular orbital coefficients and energies
    mo_coefficients = mf.mo_coeff  # MO coefficients
    mo_energies = mf.mo_energy  # MO energies

    # Determine the HOMO (highest occupied molecular orbital) energy
    num_electrons = mol.nelectron  # Total number of electrons in the system
    homo_index = num_electrons // 2 - 1  # HOMO index for closed-shell systems (0-indexed)
    homo_energy = mo_energies[homo_index] if homo_index >= 0 else None

  # Generate the cube file for the HOMO
    if homo_index >= 0:
        cube_filename = f"{atom_symbol}_HOMO.cube"
        cubegen.orbital(mol, cube_filename, mf.mo_coeff[:, homo_index])
        print(f"HOMO cube file saved as: {cube_filename}")
        
        # Visualize the cube file using py3Dmol
        cube_view = py3Dmol.view(width=400, height=400)
        with open(cube_filename, 'r') as file:
            cube_data = file.read()
        cube_view.addVolumetricData(cube_data, "cube", {'isoval': -0.03, 'color': "red", 'opacity': 0.85})
        cube_view.addVolumetricData(cube_data, "cube", {'isoval': 0.03, 'color': "blue", 'opacity': 0.85})
        cube_view.addModel(mol.tostring(format="xyz"), 'xyz')
        cube_view.setStyle({'stick': {}, "sphere": {"radius": 0.4}})
        cube_view.setBackgroundColor('0xeeeeee')
        cube_view.show()
    
    results = {
        'atom': atom_symbol,
        'total_energy': total_energy,
        'mo_coefficients': mo_coefficients,
        'mo_energies': mo_energies,
        'homo_energy': homo_energy
    }
    
    return results

# List of atoms to calculate
atoms = ['Li', 'Na']

# Store the results for each atom
results_dict = {}

# Loop over each atom and calculate orbitals and energies
for atom in atoms:
    results = calculate_orbitals_energies(atom)
    results_dict[atom] = results
    
    print(f"Results for {atom} atom:")
    print("Total Energy (Hartree):", results['total_energy'])
    print("Molecular Orbital Energies (Hartree):", results['mo_energies'])
    print("HOMO energy (Hartree):", results['homo_energy'])
    #print("Molecular Orbital Coefficients:")
    #print(results['mo_coefficients'])
    #print("\n" + "-"*50 + "\n")
    print("\n")

converged SCF energy = -7.31552598128109

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[3], line 9
      7 # Loop over each atom and calculate orbitals and energies
      8 for atom in atoms:
----> 9     results = calculate_orbitals_energies(atom)
     10     results_dict[atom] = results
     12     print(f"Results for {atom} atom:")

Cell In[2], line 42, in calculate_orbitals_energies(atom_symbol)
     40 if homo_index >= 0:
     41     cube_filename = f"{atom_symbol}_HOMO.cube"
---> 42     cubegen.orbital(mol, cube_filename, mf.mo_coeff[:, homo_index])
     43     print(f"HOMO cube file saved as: {cube_filename}")
     45     # Visualize the cube file using py3Dmol

NameError: name 'cubegen' is not defined

Hartree-Fock

Contents

Hartree-Fock#

Wavefunction#

Hartree-Fock Equations#

Fock Operator#

Self-Consistent Field (SCF) Method#

3. Total Energy of the System#

4. Strengths and Limitations#

Strengths#

Limitations#

5. Summary#

HF on example of He atom#

Practical use of HF#