Perturbation Method

Perturbation Method#

What you need to know

Perturbation method, attempts to solve analytically intractable problems by idintifying an exactly sovable part and a “small” pertrubation to it.
The method is similair in spirit to taylor expansion of continuous functions familiar to us from calculus. Just like in taylor expansion in pertrubation expansion the key is identifying the relatively small parameter in the problem to expand.
Application of pertrubation theory proceeds in two steps. Step one identify solvable part and perturbation. Part two expand energy and eigenfunctions as series of corrections of increasing order. In practice first and second order corrections to energy are sufficient to get quantiatively accurate results.
Perturbation theory allows writing down expressions entirely in terms of eigenfunctions and eigenvalues of exactly solved problem!

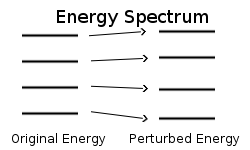
Fig. 88 Pertrubation theory quantifies how much energy levels get pertrubed by adding “small” deviation of the exactly solvable Hamiltonian. For many problems which are impossibvle to solve exactly one can still identify part of the hamiltonian as exactly solvable ${\hat{H}}^{0}$ with the rest being treated as pertrubation#

Time independent perturbations#

We have hamiltonian ${\hat{H}}_{0}$ for some exactly solvable problem think particle in a box, harmonic oscilator, etc:

{\hat{H}}^{0} ∣ n^{0} ⟩ = E_{n}^{0} ∣ n^{0} ⟩

Note the 0 superscript: It indicates exactly solvable hamitlonian, eigenfunctions and eigenvalues. The $∣ n^{0} ⟩$ is the eigenfunction corepsonding to the nth eigenvalue $E_{n}^{0}$ .
Consider a problem where we have a hamitlonian which is similiar to an exactly solvable problem differing only by a “small” pertrubation $\hat{H_{1}}$ . Small means that eiganvalues should of two systems are close relative to spacing.
The parameter $λ$ turns perturbation on $λ = 1$ and off $λ = 0$ .

\hat{H} = {\hat{H}}^{0} + λ {\hat{H}}^{1}

The objective of perturbation theory is to solve the problem with new hamiltonian expressed entirely in terms of eigenvalues and eigenfunctions of exactly solvable problems.

\hat{H} ∣ n ⟩ = E_{n} ∣ n ⟩

It’s just like Taylor expansions!#

We assume that eigenvalues and eigenfunctions can be expanded in power series in the parameter $λ$ to be set to 1 in the end.

E_{n} = E_{n}^{0} + λ E_{n}^{1} + λ^{2} E_{n}^{2} + . . .

∣ n ⟩ = ∣ n^{0} ⟩ + λ ∣ n^{1} ⟩ + λ^{2} ∣ n^{2} ⟩ . . .

Pluggin in the expansions into $\hat{H} ∣ n ⟩ = E_{n} ∣ n ⟩$ we get expression involving various terms with $λ$ . Next step is to expand brackets and group terms according to $λ^{0}$ , $λ^{1}$ , and $λ^{2}$ ,

({\hat{H}}^{0} + λ {\hat{H}}^{1}) (∣ n^{0} ⟩ + λ ∣ n^{1} ⟩ + λ^{2} ∣ n^{2} ⟩) = (E_{n}^{0} + λ E_{n}^{1} + λ^{2} E_{n}^{2}) (∣ n^{0} ⟩ + λ ∣ n^{1} ⟩ + λ^{2} ∣ n^{2} ⟩)

Pertubation equations of order $0$ , $1$ and $2$ .#

Opening the brackets and collecting different orders of $λ$ we have 0, 1 and 2nd order perturbation equations:

{\hat{H}}^{0} ∣ n^{0} ⟩ = E_{n}^{0} ∣ n^{0} ⟩

{\hat{H}}^{0} ∣ n^{1} ⟩ + \hat{H^{1}} ∣ n^{0} ⟩ = E_{n}^{0} ∣ n^{1} ⟩ + E_{n}^{1} ∣ n^{0} ⟩

\hat{H^{0}} ∣ n^{2} ⟩ + \hat{H^{1}} ∣ n^{1} ⟩ = E_{n}^{0} ∣ n^{2} ⟩ + E_{n}^{1} ∣ n^{1} ⟩ + E_{n}^{2} ∣ n^{0} ⟩

Note how the sum of upstairs indeces determines the order of perturbation expansion
The 0 order is just the exact solution.
Hamitonian only has first order expansion while eigenfunctions and eigenvalues are expanded to infinite terms. Usually going to second order is enough for most problems.

Computing pertrubation correction to energy levels#

Perturbation Approximation to Energies

E_{n} = E_{n}^{0} + H_{n n} + \sum_{k \neq n} \frac{∣ H_{n k} ∣^{2}}{E_{n}^{0} - E_{k}^{0}}

** $n$ and $k$ : Quantum numbers running from groun to excited states, e.g $n = 0, 1, 2. . .$
Matrix Elements of pertrubation

H_{n k} = ⟨ n^{0} ∣ H^{1} ∣ k^{0} ⟩

H_{n n} = ⟨ n^{0} ∣ H^{1} ∣ n^{0} ⟩

First and second order corrections to the ground state#

The first order correction to the ground state requires computing diagonal matrix elements only:

E_{0}^{(1)} = ⟨ 0 | {\hat{H}}^{1} | 0 ⟩

2nd order correction to the ground state requires calculating off-diagonal elements $H_{0 k}$ where $n = 0$ and k runs over all excited states.

E_{0}^{(2)} = \sum_{k \neq 0} \frac{∣ H_{0 k} ∣^{2}}{E_{0}^{0} - E_{k}^{0}}

Note how the energy in the denominator of 2nd order term involves difference between energy of a given state $E_{n}$ from all other states $E_{k}$ denoted by k the summation index.
Key insight If the matrix elements are of comparable magnitude the neighbouring energy levels make larger contributions to pertrubation expression.

Derivations of 1st and 2nd order corrections#

Deriving 1st order correction to energy $E_{n}^{1}$

Fixing the normalization

If we have normalization of the zero order eigenfunctions, then unperturbed eigenfunctions will be orthogonal to all higher order eigenfunctions:

⟨ n^{0} ∣ n^{0} ⟩ = 1

⟨ n^{0} ∣ n ⟩ = ⟨ n^{0} ∣ n^{0} ⟩ + λ ⟨ n^{0} ∣ n^{1} ⟩ = 1 + 0 + . . .

⟨ n^{0} ∣ n^{k} ⟩ = 0 k = 1, 2, . .

Making use of the orthogonality

{\hat{H}}^{0} ∣ n^{1} ⟩ + \hat{H^{1}} ∣ n^{0} ⟩ = E_{n}^{0} ∣ n^{1} ⟩ + E_{n}^{1} ∣ n^{0} ⟩

We multiply first order pertrubation equation by $⟨ n^{0} ∣$ and use hermitian property of Hamiltonian.

⟨ n^{0} ∣ {\hat{H}}^{0} ∣ n^{1} ⟩ + ⟨ n^{0} ∣ \hat{H^{1}} ∣ n^{0} ⟩ = E_{n}^{0} ⟨ n^{0} ∣ n^{1} ⟩ + E_{n}^{1} ⟨ n^{0} ∣ n^{0} ⟩

The first terms on the right and left hand side are zero becasue of rothogonality: $⟨ n^{0} ∣ {\hat{H}}^{0} ∣ n^{1} ⟩ = ⟨ n^{1} ∣ {\hat{H}}^{0} ∣ n^{0} ⟩ = E_{n}^{0} ⟨ n^{1} ∣ n^{0} ⟩ = 0$

First order correction

We have obtained the central result of pertrubation theory: The 1st order correction to energy $E_{n}^{1}$ .

E_{n}^{1} = ⟨ n^{0} ∣ {\hat{H}}^{1} ∣ n^{0} ⟩

E_{n} = E_{n}^{0} + E_{n}^{1} = E_{n}^{0} + ⟨ n^{0} ∣ {\hat{H}}^{1} ∣ n^{0} ⟩

Note how this expression is different from expectation expressions we have seen before. Here the eigenfunctions of ${\hat{H}}^{0}$ sandwich the the pertrubation hamitlonian ${\hat{H}}^{1}$ . The two hamitlonians in general do not share eigenfunctions!

Deriving 1st order correction to eigenfunction $∣ n^{1} ⟩$

We express the unknown first order eigenfunctions $∣ n^{1} ⟩$ in terms of known eigenfunctions $∣ k^{0} ⟩$ which becasue of Hermitian property of operators must form complete basis set.

∣ n^{1} ⟩ = \sum_{k \neq n} c_{k} ∣ k^{0} ⟩

The coefficients are $c_{k} = ⟨ k^{0} ∣ n^{1} ⟩$ . Becasue of orthogonality all terms involving eigenfunctions of nth state drop out $c_{n} = ⟨ n^{0} ∣ n^{1} ⟩ = 0$ . This is why we have indicated $k \neq n$ condition in summation expression.
Inserting the expanstion of $∣ n^{1} ⟩$ and taking dot product with bra $⟨ k^{0} ∣$ we find the coefficients of expansion:

{\hat{H}}^{0} ∣ n^{1} ⟩ + \hat{H^{1}} ∣ n^{0} ⟩ = E_{n}^{0} ∣ n^{1} ⟩ + E_{n}^{1} ∣ n^{0} ⟩

{\hat{H}}^{0} \sum_{k \neq n} c_{k} ∣ k^{0} ⟩ + \hat{H^{1}} ∣ n^{0} ⟩ = E_{n}^{0} \sum_{k \neq n} c_{k} ∣ k^{0} ⟩ + E_{n}^{1} ∣ n^{0} ⟩

c_{k} E_{k}^{0} + ⟨ k^{0} ∣ {\hat{H}}^{1} ∣ n^{0} ⟩ = c_{k} E_{n}^{0}

c_{k} = \frac{⟨ k^{0} ∣ {\hat{H}}^{1} ∣ n^{0} ⟩}{E_{n}^{0} - E_{k}^{0}} = \frac{H_{n k}}{E_{n}^{0} - E_{k}^{0}}

∣ n^{1} ⟩ = \sum_{k \neq n} c_{k} ∣ k^{0} ⟩ = \sum_{k \neq n} \frac{H_{n k}}{E_{n}^{0} - E_{k}^{0}} ∣ k^{0} ⟩

Matrix element notation

We we have introduced convenient notaation for matrix elements of pertrubed hamitlonian $H_{n k} = ⟨ k^{0} ∣ {\hat{H}}^{1} ∣ n^{0} ⟩$ . Note that hamiltonian in matrix elements is always the perturbation part.

Deriving expression for $E_{n}^{2}$

\hat{H^{0}} ∣ n^{2} ⟩ + \hat{H^{1}} ∣ n^{1} ⟩ = E_{n}^{0} ∣ n^{2} ⟩ + E_{n}^{1} ∣ n^{1} ⟩ + E_{n}^{2} ∣ n^{0} ⟩

⟨ n^{0} ∣ \hat{H^{0}} ∣ n^{2} ⟩ + ⟨ n^{0} ∣ \hat{H^{1}} ∣ n^{1} ⟩ = E^{0} ⟨ n^{0} ∣ n^{2} ⟩ + E_{n}^{1} ⟨ n^{0} ∣ n^{1} ⟩ + E_{n}^{2} ⟨ n^{0} ∣ n^{0} ⟩

E_{n}^{2} = ⟨ n^{0} ∣ {\hat{H}}^{1} ∣ n^{1} ⟩

Once again wetook dot product with bra $⟨ n^{0} ∣$ . First term on the left. is zero (hermitian+orthogonality). The firs two terms on the right are zero due to orthogonality.
We are not done yet, the expression contains eigenfunction $∣ n^{1} ⟩$ which we need to expres in terms of known solutions $∣ n^{0} ⟩$

E_{n}^{2} = ⟨ n^{0} ∣ {\hat{H}}^{1} ∣ n^{1} ⟩ = \sum_{k \neq n} c_{k} ⟨ n^{0} ∣ {\hat{H}}^{1} ∣ k^{0} ⟩ = \sum_{k \neq n} c_{k} H_{n k}

E_{n}^{2} = \sum_{k \neq n} \frac{∣ H_{n k} ∣^{2}}{E_{n}^{0} - E_{k}^{0}}

E_{n} = E_{n}^{0} + ⟨ n^{0} ∣ H^{1} ∣ n^{0} ⟩ + \sum_{k \neq n} \frac{∣ H_{n k} ∣^{2}}{E_{n}^{0} - E_{k}^{0}}

Applications#

Example-1: Estimate ground state with second order pertrubation

Write second order correction explicitely for the ground state for some exactly solvable hamiltonian $\hat{H^{0}}$ pertrubed by $\hat{H^{1}}$

E_{n} = E_{n}^{0} + H_{n n} + \sum_{k \neq n} \frac{∣ H_{n k} ∣^{2}}{E_{n}^{0} - E_{k}^{0}}

E_{0} = E_{0}^{0} + H_{00} + \frac{∣ H_{01} ∣^{2}}{E_{0}^{0} - E_{1}^{0}} + \frac{∣ H_{02} ∣^{2}}{E_{0}^{0} - E_{2}^{0}} + \frac{∣ H_{03} ∣^{2}}{E_{0}^{0} - E_{3}^{0}} + . . .

Notice that for the ground state the second order correction thereofre will always be negative because $Δ E_{0 k} = E_{0} - E_{k} < 0$

Example-2: Magnetic field

Hydrogen atom in magnetic field problem can be seen as as a hamitonian of H atom to which we have added a small pertrubation in the form of interation with magnetic field.

\hat{H} = {\hat{H}}_{0} + \frac{e}{2 m_{e}} B {\hat{L}}_{z} = {\hat{H}}_{0} + {\hat{H}}^{1}

Using 1st order pertrubation expression we can calculate for instance how ground state energy will be perturbed. Where on right hand side we define $R_{H}$ as Rydberg’s and $β_{B}$ as Bohr’s magneton, both constants.

E_{0} = E_{0}^{0} + ⟨ 0 ∣ {\hat{H}}^{1} ∣ 0 ⟩ = - \frac{R_{H}}{n^{2}} + m_{l} β_{B} B

In a similiar way the effect of spin orbit coupling ( $L S$ )

\hat{H} = {\hat{H}}_{0} + A_{S O} \hat{L} \hat{S}

E = E_{0} + A_{S O} ⟨ 0 ∣ \hat{L} \hat{S} ∣ 0 ⟩

Example-3: Perturbing particle in a box

Estimate the energy of the ground-state and first excited-state wavefunction within first-order perturbation theory of a system with the following potential energy:

V (x) = V_{0} 0 \leq x \leq \infty

V (x) = + \infty x \leq - \infty, x \geq \infty

This problem can be seen as a particle in a box pertrubed by the presence of a potential energy $V_{0}$

E_{n}^{1} = ⟨ n ∣ V_{0} ∣ n ⟩ = V_{0} \cdot \frac{2}{L} \int_{0}^{L} s i n^{2} \frac{n π x}{L} d x = V_{0}

Thus we find that energy level of PIB are pertrubed by a constant shift up term:

E_{n} = E_{n}^{0} + E_{n}^{1} \approx \frac{n^{2} h^{2}}{8 m L^{2}} + V_{0}

Example-4 Anharmonic oscillator

Anharmonic oscillator problem can be seen as a problem fo harmonic oscillator + pertrubation in the form of unharmonic term:

\hat{H} = \hat{K} + \frac{k x^{2}}{2} + γ x^{3} = {\hat{H}}_{0} + γ x^{3}

Using first order pertrubation we find an interesting result after evaluating the integral to by using simple symmetry arguments.

E_{n}^{1} = ⟨ 0 ∣ γ x^{3} ∣ n ⟩ = ⟨ e v e n / o d d ∣ o d d ∣ e v e n / o d d ⟩ = 0

But energy levels surely must experience change since we added a new term to hamitlonian. To see the change we must therefore turn to second order and use ground state as an example

E_{0}^{2} = \sum_{k \neq 0} \frac{∣ ⟨ 0 ∣ γ x^{3} ∣ k ⟩ ∣^{2}}{E_{0}^{0} - E_{k}^{0}} = \frac{∣ ⟨ 0 ∣ γ x^{3} ∣ 1 ⟩ ∣^{2}}{E_{0}^{0} - E_{1}^{0}} + \frac{∣ ⟨ n ∣ γ x^{3} ∣ 3 ⟩ ∣^{2}}{E_{0}^{0} - E_{3}^{0}} + . . .

E_{0} = E_{0} + E_{1} + E_{2} = \frac{ℏ ω}{2} + 0 + \frac{H_{01}^{2}}{ℏ ω} + \frac{H_{03}^{2}}{2 ℏ ω} + . . .

Thus we see that only terms odd terms of the sum contribute. The matrix elements need to be evaluated explicitly using Hermite polynomials.