Sympy#

  • SymPy is the main library in the SciPy ecosystem for performing symbolic mathematics, and it is suitable for a wide audience from high school students to scientific researchers.

  • SymPy like a free, open source Mathematica substitute that is built on Python and is arguably more accessible in terms of cost and ease of acquisition. All of the following SymPy code relies on the following import which makes all of the SymPy modules available.

  • Before SymPy will accept a variable as a symbol, the variable must first be defined as a SymPy symbol using the symbols() function. It takes one or more symbols at a time and attaches them to variables.

  • If you plan on using Sympy and not mixing functions from other libraries we can importing everything from sympy with the following command and not worry about attaching sympy.F to every function F

from sympy import *

x, c, m = symbols('x y a b c m')

x

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[2], line 1
----> 1 x, c, m = symbols('x y a b c m')
      3 x

ValueError: too many values to unpack (expected 3)

Common SymPy Functions#

SymPy contains an assortment of standard mathematical operators such as square root and trigonometric functions. A table of common functions is below.

Abs()

sin()

cos()

tan()

cot()

sec()

csc()

asin()

acos()

atan()

ceiling()

floor()

Min()

Max()

sqrt()

Common Algebraic Methods#

SymPy is quite capable at algebraic operations. Some of the most important ones are listed in the table below. We will focus on those

Method

Description

sympy.expand()

Expand polynomials

sympy.factor()

Factors polynomials

sympy.simplify()

Simplifies the expression

sympy.solve()

Equates the expression to zero and solves for the requested variable

sympy.subs()

Substitutes a variable for a value, expression, or another variable

sympy.series()

Expands functon in taylor series

Expand and factor#

The first steps in an algebraic manipulation

(x+1)*(x+2)*(x+3)
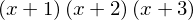
../_images/f1fa17d2cf46bd4f9a8f1a8e5b4c080b1ffd6709b0bab74aa2e48e60e8553e7c.png 
expand((x+1)*(x+2)*(x+3))
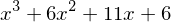
../_images/fe2fe8ad30eb36c5df2bdf9c9aab5a8a422a856629d4fd783d545c5ae0243fd9.png

The expand function takes a number of keywords arguments which we can tell the functions what kind of expansions we want to have performed. For example, to expand trigonometric expressions, use the trig=True keyword argument:

sin(a+b)
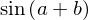
../_images/a454e1967418fa065a4873d38db140fe270af04443ffedc18926979300700386.png 
expand(sin(a+b), trig=True)
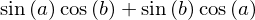
../_images/ae1628393b80ddb0dc9784f3fd6e46fbbb06f951afdd6b3ffe396dfeea98900d.png

See help(expand) for a detailed explanation of the various types of expansions the expand functions can perform.

The opposite of product expansion is of course factoring. To factor an expression in SymPy use the factor function:

factor(x**3 + 6 * x**2 + 11*x + 6)
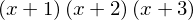
../_images/f1fa17d2cf46bd4f9a8f1a8e5b4c080b1ffd6709b0bab74aa2e48e60e8553e7c.png

Simplification#

expr = 3*x**2 - 4*x - 15 / (x - 3)

expr
\[\displaystyle 3 x^{2} - 4 x - \frac{15}{x - 3}\]
simplify(expr)
\[\displaystyle \frac{x \left(x - 3\right) \left(3 x - 4\right) - 15}{x - 3}\]

Solving equations#

expr = x**2 + 1.4*x - 5.76
expr
\[\displaystyle x^{2} + 1.4 x - 5.76\]
solve(expr)

[-3.20000000000000, 1.80000000000000]

Complex numbers#

The imaginary unit is denoted I in SymPy.

1+1*I
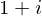
../_images/36231cd0b550a14ea3e1669a737144b4162936f58cd63938c35f5baec3595742.png 
I**2
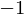
../_images/b51e8043844819f2d3fc1b18ae1287bda18488443750fce5c0faebd3bd6d66f5.png 
(x * I + 1)**2
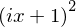
../_images/1edb819f3370fc8ee35dc7d77da928630a603fe3e1181ab4546fd39783ed3905.png

Taylor Series#

Series expansion is also one of the most useful features of a CAS. In SymPy we can perform a series expansion of an expression using the series function:

x = Symbol('x', real=True)

series(exp(x), x)
\[\displaystyle 1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6} + \frac{x^{4}}{24} + \frac{x^{5}}{120} + O\left(x^{6}\right)\]

  • By default it expands the expression around 𝑥=0 , but we can expand around any value of 𝑥 by explicitly include a value in the function call:

series(exp(x), x, 1)
\[\displaystyle e + e \left(x - 1\right) + \frac{e \left(x - 1\right)^{2}}{2} + \frac{e \left(x - 1\right)^{3}}{6} + \frac{e \left(x - 1\right)^{4}}{24} + \frac{e \left(x - 1\right)^{5}}{120} + O\left(\left(x - 1\right)^{6}; x\rightarrow 1\right)\]

And we can explicitly define to which order the series expansion should be carried out:

series(exp(x), x, 1, 4)
\[\displaystyle e + e \left(x - 1\right) + \frac{e \left(x - 1\right)^{2}}{2} + \frac{e \left(x - 1\right)^{3}}{6} + O\left(\left(x - 1\right)^{4}; x\rightarrow 1\right)\]

Differentiation#

Differentiation is usually simple. Use the diff function. The first argument is the expression to take the derivative of, and the second argument is the symbol by which to take the derivative:

y
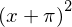
../_images/d6b7649201d89920634536e9a954b10aca6355b6b500898f8740c16dc53d7781.png 
diff(y**2, x)
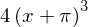
../_images/abf6f5a6a9cddef8d26910a9b7f718c8846455772de758c1faccca85ee0296c6.png

For higher order derivatives we can do:

diff(y**2, x, x)
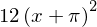
../_images/88119e971181c06a8511b18a99534f0841d25b2a1507bd4733ae05a82da4b41c.png 
diff(y**2, x, 2) # same as above
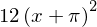
../_images/88119e971181c06a8511b18a99534f0841d25b2a1507bd4733ae05a82da4b41c.png

To calculate the derivative of a multivariate expression, we can do:

x, y, z = symbols("x,y,z")

f = sin(x*y) + cos(y*z)

\(\frac{d^3f}{dxdy^2}\)

diff(f, x, 1, y, 2)
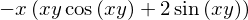
../_images/5d4db90f9eade388c44896505bda69dbd300ebba7d8154d246e1357cb9f71db3.png

Integration#

Integration is done in a similar fashion:

f
../_images/f68e9def70fb3ccbfabb11d810c66de94f92827c38c0cb8f1644ffa02d0d2304.png 
integrate(f, x)
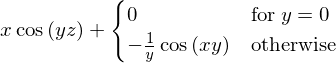
../_images/1cdc325eeb910e18186ee666ce458d722388ba23bcad33afd59dd5790124d01f.png

By providing limits for the integration variable we can evaluate definite integrals:

integrate(f, (x, -1, 1))
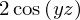
../_images/59b1273dd10ffb8bd52f56ef2924c7386db367535dd2aef1b411bb1fcc4c3e95.png

and also improper integrals

integrate(exp(-x**2), (x, -oo, oo))
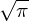
../_images/94d6b1803132d143fc9a0fbfa0d2754a94224b788753d8578975bc1939e4993d.png

Remember, oo is the SymPy notation for inifinity.

Definite Integral example

\[ \int_{0}^{\ln(4)} \frac{e^x \cdot d x} {\sqrt(e^{2x} + 9)} \]
integrate(exp(x) / sqrt(exp(2*x) + 9), (x, 0, log(4)))
\[\displaystyle - \operatorname{asinh}{\left(\frac{1}{3} \right)} + \operatorname{asinh}{\left(\frac{4}{3} \right)}\]

Sums and products#

We can evaluate sums using the function Sum:

n = Symbol("n")

Sum(1/n**2, (n, 1, 10))
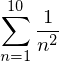
../_images/63826235758e61041b400b998201e7e18d05b7039d831c9df48f7f3e81f4a4eb.png 
Sum(1/n**2, (n,1, 10)).evalf()
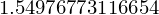
../_images/16230a96b45c35fdb5c47916bcbc1ad5b02053b713666a478c76dcba1e308dea.png 
Sum(1/n**2, (n, 1, oo)).evalf()
../_images/71f3078e8b4db5dd0b500a41a9ad9953cc9e250c37c059ed805ef0ad3ebc0e7e.png

Products work much the same way:

Product(n, (n, 1, 10)) # 10!
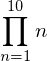
../_images/4631a83e8dca47111a5d639847c3968b30af8b6b977236fc668e7c21d1d6a9b7.png

Physics functions#

SymPy contains several physics functions. In this section, we will be working with the radial density functions (\(\psi\)) for hydrogen atomic orbitals. The squares of these functions (\(\psi ^2\)) provide the probability of finding an electron with respect to distance from the nucleus. While these equations are available in various textbooks, SymPy provides a physics module with a R_nl() function for generating these equations based on the principle (n) quantum number, angular (l) quantum number, and the atomic number (Z). For example, to generate the function for the 2p orbital of hydrogen, n = 2, l = 1, and Z = 1.

from sympy.physics.hydrogen import R_nl, Psi_nlm, E_nl

r, phi, theta = sympy.symbols('r, phi, theta')

Psi_nlm(n=3,
        l=2,
        m=0,
        r=r,
        phi=phi,
        theta=theta,
        Z=1)
\[\displaystyle \frac{2 \sqrt{30} r^{2} \cdot \left(\frac{3 \sqrt{5} \cos^{2}{\left(\theta \right)}}{4 \sqrt{\pi}} - \frac{\sqrt{5}}{4 \sqrt{\pi}}\right) e^{- \frac{r}{3}}}{1215}\]
R_nl(n=2,
     l=1,
     r=r,
     Z=1)
\[\displaystyle \frac{\sqrt{6} r e^{- \frac{r}{2}}}{12}\]

This provides the wavefunction equation with respect to the radius, r. We can also convert it to a Python function using the sympy.lambdify() method.

f = sympy.lambdify(r, R_21, modules='numpy')

This function is now callable by providing a value for r.

f(0.5)

integrate(R_21**2 * r**2, (r,0, mx)).evalf()

There is a 5.27% probability finding an electron between the nucleus and the radius of maximum probability. This is probably may be a bit surprising, but examination of the radial density plot reveals that the radius of maximum probabily is quite close to the nucleus with a significant amount of density beyond the maximum radius. Let’s see the probability of finding an electron between 0 and 10 Bohrs from the nucleus.

sympy.integrate(R_21**2 * r**2, (r,0,10)).evalf()

There is a 97.1% chance of finding the electron between 0 and 10 angstroms.

The SciPy library also includes functions in the integrate module for integrating mathematical functions.

Example problem#

As an example problem, the radius of maximum density can be found by taking the first derivative of the radial equation and solving for zero slope.

from sympy.physics.hydrogen import R_nl

r = sympy.symbols('r', real=True )

R_21 = R_nl(n=2, l=1, r=r, Z=1)

R_21
\[\displaystyle \frac{\sqrt{6} r e^{- \frac{r}{2}}}{12}\]
dR_21 = diff(R_21, r, 1)
dR_21
\[\displaystyle - \frac{\sqrt{6} r e^{- \frac{r}{2}}}{24} + \frac{\sqrt{6} e^{- \frac{r}{2}}}{12}\]
mx = float( solve(dR_21)[0] )
mx

2.0

The solve() function returns an array, so we need to index it to get the single value out. We can plot the radial density and the maximum density point to see if it worked.

f = lambdify(r, R_21, modules='numpy')

R = np.linspace(0,20,100)
plt.plot(R, f(R))
plt.plot(mx, f(mx), 'o')
plt.xlabel('Radius, $a_0$')
plt.ylabel('Probability Density');

The radius is in Bohrs (\(a_0\)) which is equal to approximately 0.53 angstroms.

Exercises#

  1. Factor the following polynomial using SymPy: \(x^2 + x – 6\)

  2. Simplify the following mathematical expression using SymPy: \( z = 3x + x^2 + 2xy \)

  3. Expand the following expression using SymPy: \((x – 2)(x + 5)(x)\)

  4. The following is the equation for the work performed by a reversible, isothermal (i.e., constant T) expansion of a piston by a fixed quantity of gas.

    \[ w = \int_{v_i}^{v_f} -nRT \frac{1}{V}dV \]

    a) Using SymPy, integrate this expression symbolically for \(V_i\) \(\rightarrow\) \(V_f\). Try having SymPy simplify the answer to see if there is a simpler form.

    b) Integrate the same express above for the expansion of 2.44 mol of He gas from 0.552 L to 1.32 L at 298 K. Feel free to use either SymPy or SciPy.