Wave function

What you need to know

1. The Probabilistic Nature of the Quantum World
   The quantum realm operates on fundamentally probabilistic principles, where certainty is replaced by probabilities.

2. Wave Function and Probability Distribution
   The absolute square of the wave function, \(|\psi|^2\), represents the probability distribution of finding a quantum particle in space and time.

What is the meaning of a wave-function \(\psi\) ?

• In the classical wave equation, the wave function has a clear mechanical interpretation: it represents the degree of disturbance in the wave. For example, it can describe the elevation of a guitar string from its resting position.

• In contrast, the quantum wave function is less intuitive. The wave function itself does not have direct physical meaning, as it is generally a complex function. To connect it to measurable quantities, we need to extract real values from it that correspond to physical observables.

• The key insight is that the absolute square of the wave function gives the probability distribution:

Probabilistic meaning of quantum wave function (square)

\[p(x) = \psi^{*}(x) \cdot \psi(x) = |\psi(x)|^2\]

• \(p(x)\) is a probability distribution function. It is describing the likelihood of finding a quantum object at a positions x.

• \(p(x)dx\) gives the probability to find particle in a tiny part of space inside \(x, x+dx\) interval.

• In three-dimensional space, the analogous expression is:

  \[p(x, y, z) = \psi(x, y, z)^{*} \cdot \psi(x, y, z)\]

Probability Refresher

• Before introducing quantum mechanics and wavefunctions, let’s recall some core ideas from probability.

Random Variables

• A random variable assigns numbers to the outcomes of an experiment. E.g how many squirrels you see every day is a random variable.

• Discrete examples: dice rolls, coin flips.

• Continuous examples: particle position, measurement noise.

Probability Distributions

• A continuous random variable is fully described by a distribution of all posisble values. We call this object a probability distributions \(p(x)\) which must be integrated (summed in case of discrete) to one showing that we cover all possibilities and that each possibility is assigned a fraction of 1.

Rules of Probabilities

• Non-negative:

\[p(x) \geq 0\]

• Normalized:

\[\int_{-\infty}^{\infty} p(x)\,dx = 1\]

• Mean (expectation):

  \[ \mu = \langle x \rangle = \int_{-\infty}^{\infty} x\,p(x)\,dx \]

• Variance:

  \[ \sigma^2 = \langle x^2 \rangle - \langle x \rangle^2 \]

Further Exploration

• Video overview

• Interactive probability explorer

Worked Examples of Probability distributions

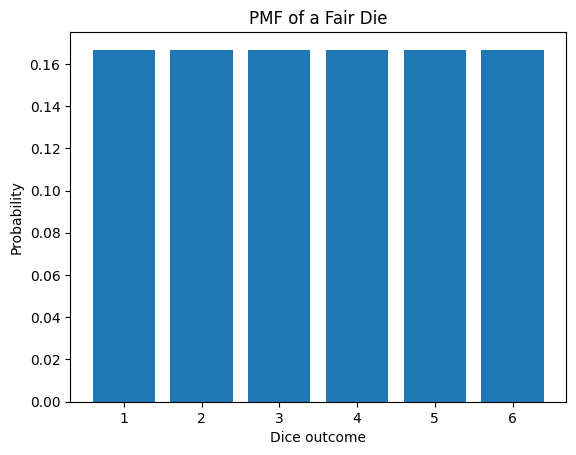
1. Fair coin Flip

• Random variable \(X \in \{0,1\}\) with

\[ P(X=0) = 0.5, \quad P(X=1) = 0.5 \]

Normalization

\[ P(0)+P(1) = 0.5+0.5 = 1 \]

Mean

\[ \langle X \rangle = \sum_x xP(x) = 0\cdot 0.5 + 1\cdot 0.5 = 0.5 \]

Variance

\[ \langle X^2 \rangle = 0^2\cdot 0.5 + 1^2\cdot 0.5 = 0.5 \]

\[ \sigma^2 = \langle X^2 \rangle - \langle X \rangle^2 = 0.5 - (0.5)^2 = 0.25 \]

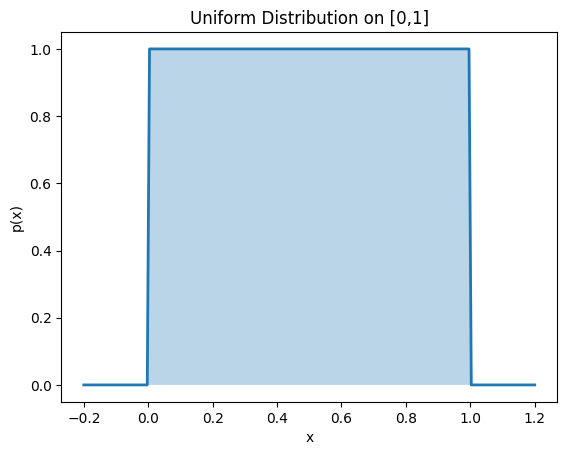
2. Uniform Distribution on [0,1]

• PDF: $\( p(x) = \begin{cases} 1, & 0 \leq x \leq 1 \\ 0, & \text{otherwise} \end{cases} \)$

Normalization

\[ \int_0^1 1 \, dx = 1 \]

Mean

\[ \langle x \rangle = \int_0^1 x \, dx = \left.\frac{x^2}{2}\right|_0^1 = \frac{1}{2} \]

Variance

\[ \langle x^2 \rangle = \int_0^1 x^2 \, dx = \left.\frac{x^3}{3}\right|_0^1 = \frac{1}{3} \]

\[ \sigma^2 = \frac{1}{3} - \left(\frac{1}{2}\right)^2 = \frac{1}{12} \]

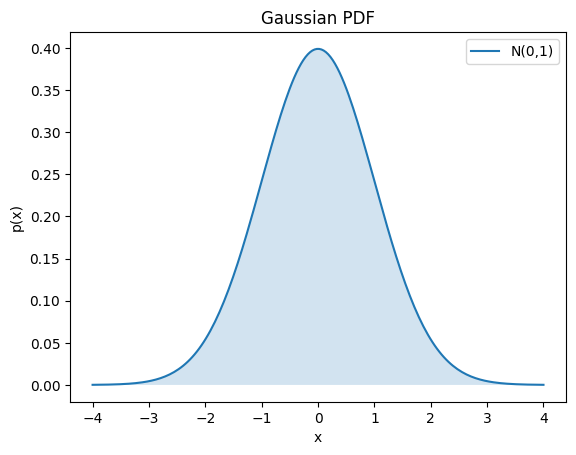
Gaussian Distribution \(\mathcal{N}(0,1)\)

• PDF: $\( p(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2} \)$

Normalization

\[ \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-x^2/2} dx = 1 \]

(This is the famous Gaussian integral.)

Mean

\[ \langle x \rangle = \int_{-\infty}^\infty x\,p(x)\,dx = 0 \quad \text{(odd function)} \]

Variance

\[ \langle x^2 \rangle = \int_{-\infty}^\infty x^2 \frac{1}{\sqrt{2\pi}} e^{-x^2/2}\,dx = 1 \]

\[ \sigma^2 = 1 - 0^2 = 1 \]

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Discrete probabilities (fair dice)
outcomes = np.arange(1, 7)
probs = np.ones_like(outcomes) / 6

plt.bar(outcomes, probs)
plt.xlabel("Dice outcome")
plt.ylabel("Probability")
plt.title("PMF of a Fair Die")
plt.show()

Show code cell source Hide code cell source

# Continuous uniform distribution on [a,b]
a, b = 0, 1
x = np.linspace(-0.2, 1.2, 200)
pdf = np.where((x >= a) & (x <= b), 1/(b-a), 0)

plt.plot(x, pdf, lw=2)
plt.fill_between(x, pdf, alpha=0.3)
plt.xlabel("x")
plt.ylabel("p(x)")
plt.title("Uniform Distribution on [0,1]")
plt.show()

Show code cell source Hide code cell source

from scipy.stats import norm

x = np.linspace(-4, 4, 200)
pdf = norm.pdf(x, loc=0, scale=1)

plt.plot(x, pdf, label="N(0,1)")
plt.fill_between(x, pdf, alpha=0.2)
plt.xlabel("x")
plt.ylabel("p(x)")
plt.title("Gaussian PDF")
plt.legend()
plt.show()

Show code cell source Hide code cell source

# -----------------------------
# Correct sampling for H-atom 1s
# -----------------------------
N = 6000
a0 = 1.0

# For 1s: if x = 2r/a0, then x ~ Gamma(k=3, theta=1)
x = np.random.gamma(shape=3.0, scale=1.0, size=N)
r = 0.5 * a0 * x

# Isotropic angles
u = np.random.rand(N)
theta = np.arccos(1 - 2*u)
phi = 2*np.pi*np.random.rand(N)

# Convert to Cartesian and take a 2D projection
x3 = r * np.sin(theta) * np.cos(phi)
y3 = r * np.sin(theta) * np.sin(phi)

# Histogram for the shell probability density P(r) (per unit r)
bins = np.linspace(0, 6*a0, 80)
hist, edges = np.histogram(r, bins=bins, density=True)
centers = 0.5*(edges[1:] + edges[:-1])

# Analytical radial distribution P(r) = 4 r^2 |psi|^2 = 4 r^2 / (a0^3*pi) * exp(-2r/a0) * pi
# Simplifies to: P(r) = (4/a0^3) r^2 exp(-2r/a0), which integrates to 1
rr = np.linspace(0, bins[-1], 400)
P_r = (4.0/(a0**3)) * rr**2 * np.exp(-2*rr/a0)

# Side-by-side subplots: dot cloud and radial distribution

fig, axs = plt.subplots(1, 2, figsize=(12, 5))

# Left: simulated dot cloud
axs[0].scatter(x3, y3, s=1, alpha=0.5)
axs[0].set_title("Hydrogen 1s: position observations (2D projection)")
axs[0].set_xlabel("x [$a_0$]")
axs[0].set_ylabel("y [$a_0$]")
axs[0].set_aspect('equal')

# Right: radial distribution histogram + analytical curve
axs[1].plot(centers, hist, lw=2, label="Monte Carlo (histogram)")
axs[1].plot(rr, P_r, lw=2, linestyle="--", label="Analytical 1s")
axs[1].set_title("Radial probability distribution")
axs[1].set_xlabel("r [$a_0$]")
axs[1].set_ylabel("$P(r)$")
axs[1].legend()

plt.tight_layout()
plt.show()

Normalization of wavefunction

• For the wave function to represent a proper probability distribution, it must be normalizable. If it is not normalizable, the wave function is only proportional to a probability distribution and not equal to it.

• Normalization of \(\psi^2\) ensures that there is absolute certainty that the quantum object exists somewhere in space. In an experiment, when searching for a quantum particle across the entire space, normalization guarantees that you will find it somewhere.

• Normalization in 1D:

  \[\int^{+\infty}_{-\infty} |\psi(x)|^2 dx = \int^{+\infty}_{-\infty} p(x) dx = 1\]

• To normalize a wave function \(\psi'\), multiply it by a constant: \(\psi = N\psi'\). The constant \(N\) is determined by plugging this expression into the normalization condition. In other words, normalization helps determine the multiplicative factor in front of wave functions.

• Normalization in 3D:

  \[\int^{+\infty}_{-\infty} \int^{+\infty}_{-\infty} \int^{+\infty}_{-\infty} |\psi(x, y, z)|^2 dx \, dy \, dz = 1\]

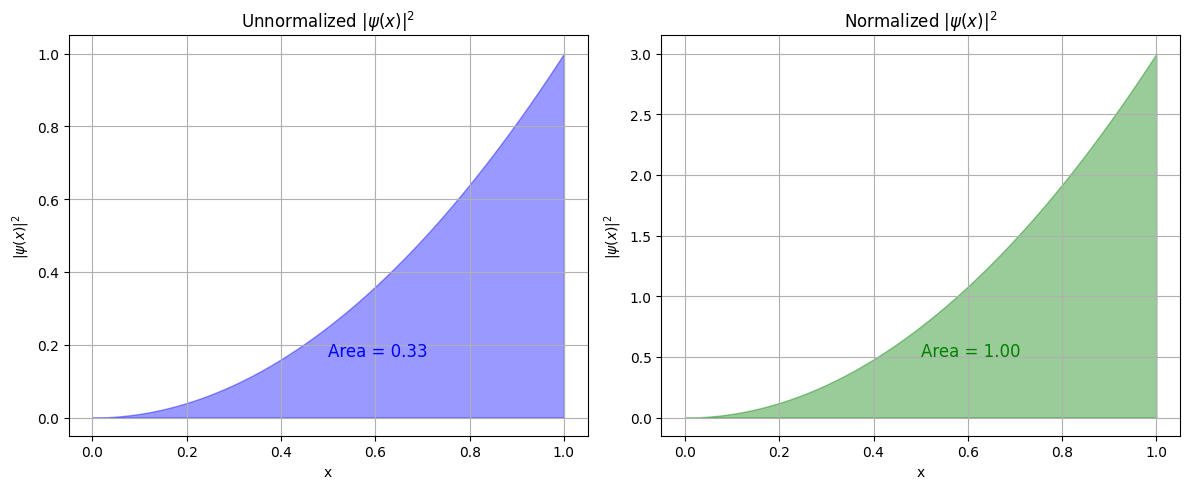
Normalization example

• Given the wave function \(\psi(x)=x\) on the range \([0,1]\), normalize it so that it becomes a proper probability distribution function.

We require

\[ \int_0^1 |\psi(x)|^2 \, dx = 1. \]

Substitute \(\psi(x)=C\,x\):

\[ \int_0^1 (C\,x)^2 \, dx = 1, \]

\[ C^2 \int_0^1 x^2 \, dx = 1, \]

\[ C^2 \cdot \frac{1}{3} = 1. \]

\[ C^2 = 3 \quad \Rightarrow \quad C = \sqrt{3}. \]

Therefore the normalized wave function is

\[ \psi(x) = \sqrt{3}\,x, \quad 0 \leq x \leq 1. \]

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Define x values
x = np.linspace(0, 1, 500)

# Unnormalized psi
psi_unnorm = x
psi2_unnorm = psi_unnorm**2

# Normalized psi (C = sqrt(3))
psi_norm = np.sqrt(3) * x
psi2_norm = psi_norm**2

# Compute integrals for annotation
area_unnorm = np.trapz(psi2_unnorm, x)
area_norm = np.trapz(psi2_norm, x)

# Create the figure and axes
fig, axes = plt.subplots(1, 2, figsize=(12, 5))

# --- Plot 1: Unnormalized psi² ---
axes[0].fill_between(x, psi2_unnorm, alpha=0.4, color="blue")
axes[0].set_title("Unnormalized $|\psi(x)|^2$")
axes[0].set_xlabel("x")
axes[0].set_ylabel(r"$|\psi(x)|^2$")
axes[0].grid(True)
axes[0].text(0.5, 0.2, rf"Area = {area_unnorm:.2f}", 
             transform=axes[0].transAxes, fontsize=12, color="blue")

# --- Plot 2: Normalized psi² ---
axes[1].fill_between(x, psi2_norm, alpha=0.4, color="green")
axes[1].set_title("Normalized $|\psi(x)|^2$")
axes[1].set_xlabel("x")
axes[1].set_ylabel(r"$|\psi(x)|^2$")
axes[1].grid(True)
axes[1].text(0.5, 0.2, rf"Area = {area_norm:.2f}", 
             transform=axes[1].transAxes, fontsize=12, color="green")

plt.tight_layout()
plt.show()

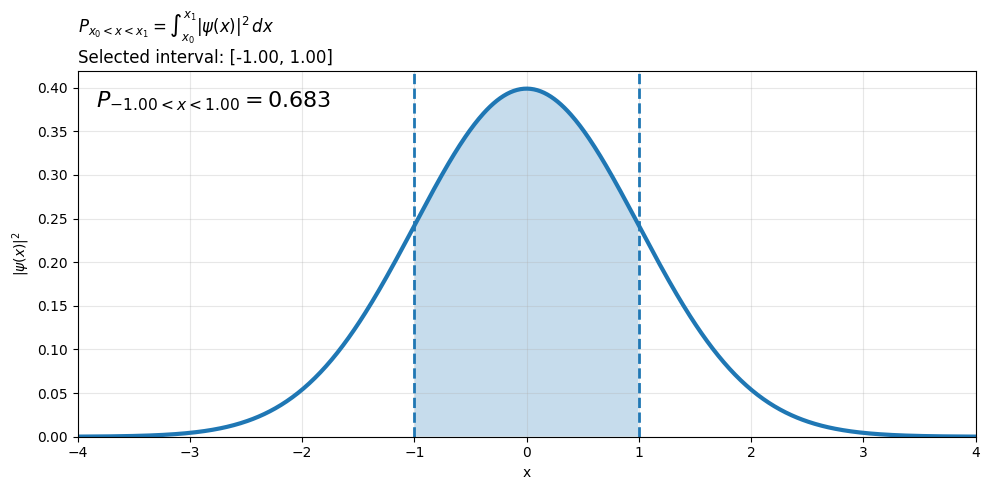
What can we do with probability distribution functions (PDF)?

• By definition probability distribution function \(p(x) \) allows quantifying various probabilities that a quantum “particle” is located in an infinitesimal slice \([x, x+dx]\) around point \(x\). This then enables us to find probabilities in any finite region \([a,b]\) simply by integrating:

  \[p(a<x<b)=\int_a^b |\psi(x)|^2dx\]

• In higher dimensions, e.g. 3D, we can locate particle around volume \(dxdydz\) or any finite volume via a similar integration:

  \[p(a_x<x<b_x,a_y<y<b_y, a_z<z<b_z )=\int^{b_x}_{a_x} \int^{b_y}_{a_y} \int^{b_z}_{a_z} |\psi(x,y,z)|^2dx dy dz\]

What about quantities which correspond to operators?

• Recall that mean value of x is computed by weighting its values by probabilities, e.g think of average mass of box of candies, we multiply probability or fraction of each candy type by its mass and sum.

\[\langle x \rangle = x_1 p_2+x_2 p_2 + ...\]

\[\langle x \rangle = \int x\cdot p(x) dx\]

• Likewise you can compute averge of any function of x, say \(x^2\) or \(sin(x)\).

\[\langle f \rangle = \int f(x) \cdot p(x) dx\]

• For quantities like momentum or total energy which are no longer simple functions as in classical mechanics but operators, \(\hat{p}\) and \(\hat{H}\), we simply have to use operators in the defintion of moments!

\[\langle A \rangle = \int \hat{A} p(x) \cdot dx = \int \psi^{*}(x) \cdot \hat{A} \psi(x) \cdot dx \]

Average quantity	Corresponding operator
\(\langle E \rangle=\int \psi^{*}(x) \hat{H} \psi(x) dx\)	\(\hat{H}=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)\)
\(\langle K \rangle=\int \psi^{*}(x) \hat{K}\psi(x) dx \)	\(\hat{K}=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\)
\(\langle p \rangle=\int \psi^{*}(x) \hat{p} \psi(x) dx\)	\(\hat{p}=-i\hbar\frac{d}{dx}\)
\(\langle p^2 \rangle=\int \psi^{*}(x) \hat{p}^2 \psi(x) dx\)	\(\hat{p}^2=-\hbar^2\frac{d^2}{dx^2}\)

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from math import erf, sqrt

# ----- Parameters -----
sigma = 1.0  # width of the Gaussian (harmonic oscillator ground state)
x0, x1 = -1.0, 1.0  # interval to integrate over

# ----- Define |psi(x)|^2 for a normalized Gaussian -----
def prob_density(x, sigma):
    # |psi(x)|^2 = (1/(sqrt(2*pi)*sigma)) * exp(-x^2/(2*sigma^2))
    return (1.0/(np.sqrt(2*np.pi)*sigma)) * np.exp(-x**2/(2*sigma**2))

# Probability via the error function (analytic CDF of a normal distribution)
def interval_probability(a, b, sigma):
    return 0.5*(erf(b/(sqrt(2)*sigma)) - erf(a/(sqrt(2)*sigma)))

P = interval_probability(x0, x1, sigma)

# ----- Plot -----
xs = np.linspace(-4*sigma, 4*sigma, 800)
ys = prob_density(xs, sigma)

fig = plt.figure(figsize=(10, 5))

# Title with the integral expression
plt.title(r"$P_{x_0<x<x_1}=\int_{x_0}^{x_1}|\psi(x)|^2\,dx$" + 
          f"\nSelected interval: [{x0:.2f}, {x1:.2f}]",
          loc="left")

# Curve
plt.plot(xs, ys, linewidth=3)

# Shade between x0 and x1 under the curve
mask = (xs >= x0) & (xs <= x1)
plt.fill_between(xs[mask], ys[mask], 0, alpha=0.25)

# Mark the boundaries with vertical dashed lines
plt.axvline(x0, linestyle="--", linewidth=2)
plt.axvline(x1, linestyle="--", linewidth=2)

# Tick marks and labels
plt.xlabel("x")
plt.ylabel(r"$|\psi(x)|^2$")

# Annotate the probability
plt.text(0.02, 0.90, rf"$P_{{{x0:.2f}<x<{x1:.2f}}} = {P:.3f}$",
         transform=plt.gca().transAxes, fontsize=16)

plt.xlim(xs.min(), xs.max())
plt.ylim(bottom=0)
plt.grid(True, alpha=0.3)
plt.tight_layout()

out_path = "/mnt/data/interval_probability_demo.png"
plt.savefig(out_path, dpi=200)
plt.show()

out_path

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
Cell In[6], line 56
     53 plt.tight_layout()
     55 out_path = "/mnt/data/interval_probability_demo.png"
---> 56 plt.savefig(out_path, dpi=200)
     57 plt.show()
     59 out_path

File /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/matplotlib/pyplot.py:1023, in savefig(*args, **kwargs)
   1020 @_copy_docstring_and_deprecators(Figure.savefig)
   1021 def savefig(*args, **kwargs):
   1022     fig = gcf()
-> 1023     res = fig.savefig(*args, **kwargs)
   1024     fig.canvas.draw_idle()  # Need this if 'transparent=True', to reset colors.
   1025     return res

File /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/matplotlib/figure.py:3378, in Figure.savefig(self, fname, transparent, **kwargs)
   3374     for ax in self.axes:
   3375         stack.enter_context(
   3376             ax.patch._cm_set(facecolor='none', edgecolor='none'))
-> 3378 self.canvas.print_figure(fname, **kwargs)

File /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/matplotlib/backend_bases.py:2366, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2362 try:
   2363     # _get_renderer may change the figure dpi (as vector formats
   2364     # force the figure dpi to 72), so we need to set it again here.
   2365     with cbook._setattr_cm(self.figure, dpi=dpi):
-> 2366         result = print_method(
   2367             filename,
   2368             facecolor=facecolor,
   2369             edgecolor=edgecolor,
   2370             orientation=orientation,
   2371             bbox_inches_restore=_bbox_inches_restore,
   2372             **kwargs)
   2373 finally:
   2374     if bbox_inches and restore_bbox:

File /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/matplotlib/backend_bases.py:2232, in FigureCanvasBase._switch_canvas_and_return_print_method.<locals>.<lambda>(*args, **kwargs)
   2228     optional_kws = {  # Passed by print_figure for other renderers.
   2229         "dpi", "facecolor", "edgecolor", "orientation",
   2230         "bbox_inches_restore"}
   2231     skip = optional_kws - {*inspect.signature(meth).parameters}
-> 2232     print_method = functools.wraps(meth)(lambda *args, **kwargs: meth(
   2233         *args, **{k: v for k, v in kwargs.items() if k not in skip}))
   2234 else:  # Let third-parties do as they see fit.
   2235     print_method = meth

File /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/matplotlib/backends/backend_agg.py:509, in FigureCanvasAgg.print_png(self, filename_or_obj, metadata, pil_kwargs)
    462 def print_png(self, filename_or_obj, *, metadata=None, pil_kwargs=None):
    463     """
    464     Write the figure to a PNG file.
    465 
   (...)
    507         *metadata*, including the default 'Software' key.
    508     """
--> 509     self._print_pil(filename_or_obj, "png", pil_kwargs, metadata)

File /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/matplotlib/backends/backend_agg.py:458, in FigureCanvasAgg._print_pil(self, filename_or_obj, fmt, pil_kwargs, metadata)
    453 """
    454 Draw the canvas, then save it using `.image.imsave` (to which
    455 *pil_kwargs* and *metadata* are forwarded).
    456 """
    457 FigureCanvasAgg.draw(self)
--> 458 mpl.image.imsave(
    459     filename_or_obj, self.buffer_rgba(), format=fmt, origin="upper",
    460     dpi=self.figure.dpi, metadata=metadata, pil_kwargs=pil_kwargs)

File /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/matplotlib/image.py:1689, in imsave(fname, arr, vmin, vmax, cmap, format, origin, dpi, metadata, pil_kwargs)
   1687 pil_kwargs.setdefault("format", format)
   1688 pil_kwargs.setdefault("dpi", (dpi, dpi))
-> 1689 image.save(fname, **pil_kwargs)

File /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/PIL/Image.py:2563, in Image.save(self, fp, format, **params)
   2561         fp = builtins.open(filename, "r+b")
   2562     else:
-> 2563         fp = builtins.open(filename, "w+b")
   2564 else:
   2565     fp = cast(IO[bytes], fp)

FileNotFoundError: [Errno 2] No such file or directory: '/mnt/data/interval_probability_demo.png'

Example of using probabilsitic calculations in QM

Example 1 — Probability in a region (1D)

Take the normalized wavefunction on \([0,1]\): \(\psi(x)=\sqrt{3}\,x\). Then \(p(x)=|\psi(x)|^2=3x^2\).

• Probability that the particle lies in \([a,b]\subset[0,1]\):

\[ P(a<x<b)=\int_a^b 3x^2\,dx= \left[x^3\right]_a^b=b^3-a^3. \]

• Concrete numbers, say \([0.3,0.6]\):

\[ P(0.3<x<0.6)=0.6^3-0.3^3=0.216-0.027=0.189. \]

Example 2 — 3D slice probability (separable state)

Let \(\psi(x,y,z)=\sqrt{27}\,xyz\) on the unit cube \([0,1]^3\) (this is normalized since \(|\psi|^2=27x^2y^2z^2\) and \(\int_0^1 x^2dx=\tfrac13\), so \(27(\tfrac13)^3=1\)).

• Probability the particle is inside the rectangular box \([a_x,b_x]\times[a_y,b_y]\times[a_z,b_z]\):

\[ P=\int_{a_x}^{b_x}\!\!\int_{a_y}^{b_y}\!\!\int_{a_z}^{b_z}27x^2y^2z^2\,dz\,dy\,dx = \big(b_x^3-a_x^3\big)\big(b_y^3-a_y^3\big)\big(b_z^3-a_z^3\big). \]

Example 3 — Averages and variance from a PDF

For \(\psi(x)=\sqrt{3}\,x\) on \([0,1]\) (so \(p(x)=3x^2\)):

• Mean position:

\[ \langle x\rangle=\int_0^1 x\,3x^2\,dx=3\int_0^1 x^3dx=\tfrac34. \]

• Mean square position:

\[ \langle x^2\rangle=\int_0^1 x^2\,3x^2\,dx=3\int_0^1 x^4dx=\tfrac35. \]

• Variance and standard deviation:

\[ \mathrm{Var}(x)=\langle x^2\rangle-\langle x\rangle^2=\tfrac35-\Big(\tfrac34\Big)^2=\tfrac{3}{80},\qquad \sigma_x=\sqrt{\tfrac{3}{80}}\approx 0.1937. \]

Example 4 — Operator expectations (momentum/energy in a box)

Operator rules:

• \( \hat{p}=-i\hbar\,\dfrac{d}{dx}\),

• \( \hat{H}=-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2}+V(x)\).

Use the infinite square well on \([0,1]\) with \(V(x)=0\) inside and \(\psi_n(x)=\sqrt{2}\sin(n\pi x)\), which is normalized.

• Momentum expectation:

\[ \langle p\rangle=\int_0^1\psi_n^*(-i\hbar)\psi_n'\,dx=0 \]

(the integrand is odd over a full sine half-wave, or integrate by parts with vanishing boundary terms).

• Momentum squared:

\[ \langle p^2\rangle=\int_0^1\psi_n^*(-\hbar^2)\psi_n''\,dx =(n\pi\hbar)^2. \]

• Energy (since \(\hat{H}=\hat{p}^2/2m\) inside the well):

\[ \langle E\rangle=\frac{\langle p^2\rangle}{2m}=\frac{(n\pi\hbar)^2}{2m}. \]