Orbitals of homonuclear diatomic molecules#
Which atomic orbitals mix to form molecular orbitals and what are their relative energies? The graph on the left can be used to obtain the energy order of molecular orbitals and indicates the atomic orbital limits.
The non-crossing rule: States with the same symmetry never cross.#
Bonding orbitals: |
\(1\sigma_g\), \(2\sigma_g\), \(1\pi_u\), etc. |
|---|---|
Antibonding orbitals: |
\(1\sigma_u^*\), \(2\sigma_u^*\), \(1\pi_g^*\), etc. |
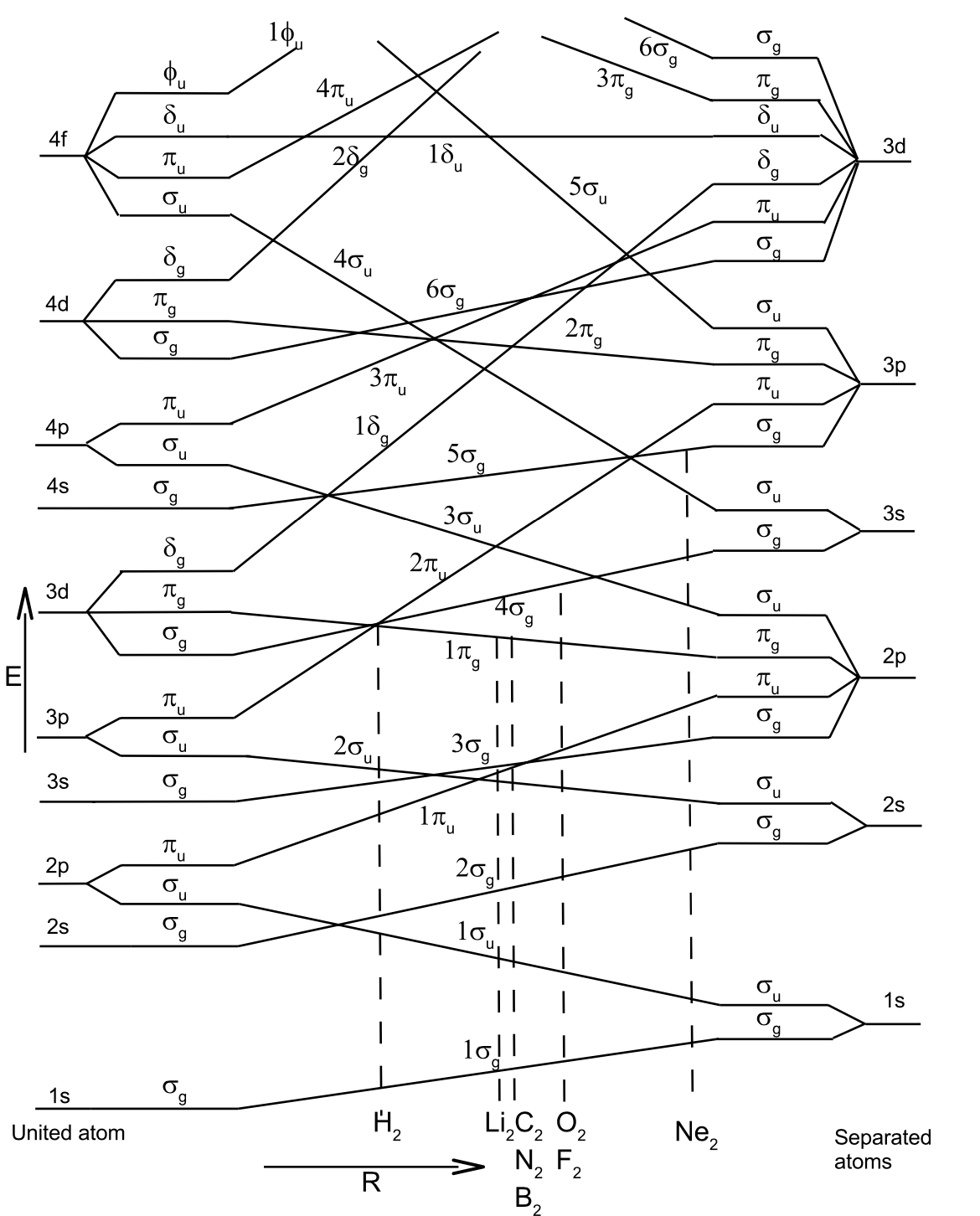
Table of MOs#
The orbitals should be filled with electrons in the order of increasing energy. Note that \(\pi\), \(\delta\), etc. orbitals can hold a total of 4 electrons. If only one bond is formed, we say that the bond order (BO) is 1. If two bonds form (for example, one \(\sigma\) and one \(\pi\)), we say that the bond order is 2 (double bond). Molecular orbitals always come in pairs: bonding and antibonding.
Molecule |
# of els. |
El. Conf. |
Term sym. |
BO |
\(R_e\) (\(\AA\)) |
\(D_e\) (eV) |
|---|---|---|---|---|---|---|
\(H_2^+\) |
1 |
\((1\sigma_g)\) |
\(^2\Sigma_g\) |
0.5 |
1.060 |
2.793 |
\(H_2\) |
2 |
\((1\sigma_g)^2\) |
\(^1\Sigma_g\) |
1.0 |
0.741 |
4.783 |
\(He_2^+\) |
3 |
\((1\sigma_g)^2(1\sigma_u)\) |
\(^2\Sigma_u\) |
0.5 |
1.080 |
2.5 |
\(He_2\) |
4 |
\((1\sigma_g)^2(1\sigma_u)^2\) |
\(^1\Sigma_g\) |
0.0 |
||
\(Li_2\) |
6 |
\(He_2(2\sigma_g)^2\) |
\(^1\Sigma_g\) |
1.0 |
2.673 |
1.14 |
\(Be_2\) |
8 |
\(He_2(2\sigma_g)^2(2\sigma_u)^2\) |
\(^1\Sigma_g\) |
0.0 |
||
\(B_2\) |
10 |
\(Be_2(1\pi_u)^2\) |
\(^3\Sigma_g\) |
1.0 |
1.589 |
\(\approx 3.0\) |
\(C_2\) |
12 |
\(Be_2(1\pi_u)^4\) |
\(^1\Sigma_g\) |
2.0 |
1.242 |
6.36 |
\(N_2^+\) |
13 |
\(Be_2(1\pi_u)^4(3\sigma_g)\) |
\(^2\Sigma_g\) |
2.5 |
1.116 |
8.86 |
\(N_2\) |
14 |
\(Be_2(1\pi_u)^4(3\sigma_g)^2\) |
\(^1\Sigma_g\) |
3.0 |
1.094 |
9.902 |
\(O_2^+\) |
15 |
\(N_2(1\pi_g)\) |
\(^2\Pi_g\) |
2.5 |
1.123 |
6.77 |
\(O_2\) |
16 |
\(N_2(1\pi_g)^2\) |
\(^3\Sigma_g\) |
2.0 |
1.207 |
5.213 |
\(F_2\) |
18 |
\(N_2(1\pi_g)^4\) |
\(^1\Sigma_g\) |
1.0 |
1.435 |
1.34 |
\(Ne_2\) |
20 |
\(N_2(1\pi_g)^4(3\sigma_u)^2\) |
\(^1\Sigma_g\) |
0.0 |
When value of \(R_0\) not shown means molecular is not stable
Note that the Hund’s rules predict that the electron configuration with the largest multiplicity lies the lowest in energy when the highest occupied MOs are degenerate.